Oceń, czy podane zdania są prawdziwe czy fałszywe dla paraboli
![]() .
.
A. Prosta
![]() przechodzi przez wierzchołek tej paraboli.
przechodzi przez wierzchołek tej paraboli.
B. Prosta
![]() jest osią symetrii tej paraboli.
jest osią symetrii tej paraboli.
C. Prosta
![]() nie ma z tą parabolą punktów wspólnych.
nie ma z tą parabolą punktów wspólnych.
Wierzchołek paraboli:
![]()
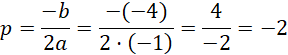
![]()
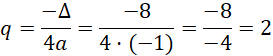
Zatem:
![]()
Zdania A i B są prawdziwe.
Dziedziną podanej paraboli są liczby rzeczywiste, zatem parabola przecina się z prostą
![]() .
.
Zdanie C jest fałszywe.

Zdania A i B: Najpierw wyznacz wierzchołek paraboli dla podanej funkcji kwadratowej. Skorzystaj z zależności, że dla funkcji kwadratowej w postaci ogólnej
![]() parabola ma wierzchołek w punkcie
parabola ma wierzchołek w punkcie
![]() . Współrzędne p i q możemy wyznaczyć ze wzorów:
. Współrzędne p i q możemy wyznaczyć ze wzorów:
![]() oraz
oraz
![]() , gdzie
, gdzie
![]() to tak zwany wyróżnik funkcji, który możemy obliczyć ze wzoru:
to tak zwany wyróżnik funkcji, który możemy obliczyć ze wzoru:
![]() . Następnie zauważ, że aby prosta
. Następnie zauważ, że aby prosta
![]() przechodziła przez wierzchołek paraboli, to druga współrzędna wierzchołka musi być równa 2. Analogicznie, aby prosta
przechodziła przez wierzchołek paraboli, to druga współrzędna wierzchołka musi być równa 2. Analogicznie, aby prosta
![]() była osią symetrii paraboli, to pierwsza współrzędna wierzchołka musi być równa -2.
była osią symetrii paraboli, to pierwsza współrzędna wierzchołka musi być równa -2.
Zdanie C: Zauważ, że funkcja opisana na zbiorze liczb rzeczywistych przecina się z każdą prostą
![]() , gdzie b to dowolna liczba rzeczywista.
, gdzie b to dowolna liczba rzeczywista.

Zadanie 1.4
407Zadanie 1.5
407Zadanie 1.6
407Zadanie 1.7
407Zadanie 1.8
408Zadanie 1.10
408Zadanie 1.11
408Zadanie 1.16
409Zadanie 2.4
414Zadanie 2.5
414Zadanie 2.6
414Zadanie 2.7
415Zadanie 2.8
415Zadanie 2.9
415Zadanie 2.10
415Zadanie 2.11
415Zadanie 2.12
415Zadanie 2.13
415Zadanie 2.14
416Zadanie 2.18
416Zadanie 2.19
416Zadanie 2.20
416Zadanie 2.21
416Zadanie 2.22
417Zadanie 2.23
417Zadanie 3.8
423Zadanie 3.9
423Zadanie 3.10
423Zadanie 3.11
423Zadanie 3.12
423Zadanie 3.13
424Zadanie 3.14
424Zadanie 3.15
424Zadanie 3.16
424Zadanie 3.20
424Zadanie 3.23
425Zadanie 3.24
425Zadanie 4.22
430Zadanie 4.23
430Zadanie 4.24
430Zadanie 4.27
431Zadanie 4.30
431Zadanie 4.32
431Zadanie 4.35
431Zadanie 4.41
432Zadanie 4.42
432
