Spośród podanych wybierz wartość współczynnika b, dla której parabola o równaniu
![]() ma tylko jeden punkt wspólny z osią x.
ma tylko jeden punkt wspólny z osią x.
A.
![]()
B.
![]()
C.
![]()
D. Nie istnieje takie b.
Wierzchołek paraboli:
![]()
Skoro parabola ma tylko jeden punkt wspólny z osią x, to wierzchołek tej paraboli musi leżeć na osi x.
Zatem:
![]()
Żeby q było równe zero, musi zachodzić zależność:
![]()
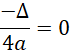
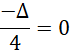
![]()
Czyli:
![]()
![]()
![]()
Zatem:
![]()
Odp.: B.
![]()

Zauważ, że żeby oś x miała tylko jeden punkt wspólny z parabolą, wierzchołek tej paraboli musi leżeć na osi x. Zatem druga współrzędna
![]() musi być równa zero. Wyznacz, dla jakiego b jest to prawdą. Skorzystaj ze wzorów
musi być równa zero. Wyznacz, dla jakiego b jest to prawdą. Skorzystaj ze wzorów
![]() i
i
![]() , gdzie a, b i c to współczynniki funkcji kwadratowej
, gdzie a, b i c to współczynniki funkcji kwadratowej
![]() .
.

Zadanie 1.4
407Zadanie 1.5
407Zadanie 1.6
407Zadanie 1.7
407Zadanie 1.8
408Zadanie 1.10
408Zadanie 1.11
408Zadanie 1.16
409Zadanie 2.4
414Zadanie 2.5
414Zadanie 2.6
414Zadanie 2.7
415Zadanie 2.8
415Zadanie 2.9
415Zadanie 2.10
415Zadanie 2.11
415Zadanie 2.12
415Zadanie 2.13
415Zadanie 2.14
416Zadanie 2.18
416Zadanie 2.19
416Zadanie 2.20
416Zadanie 2.21
416Zadanie 2.22
417Zadanie 2.23
417Zadanie 3.8
423Zadanie 3.9
423Zadanie 3.10
423Zadanie 3.11
423Zadanie 3.12
423Zadanie 3.13
424Zadanie 3.14
424Zadanie 3.15
424Zadanie 3.16
424Zadanie 3.20
424Zadanie 3.23
425Zadanie 3.24
425Zadanie 4.22
430Zadanie 4.23
430Zadanie 4.24
430Zadanie 4.27
431Zadanie 4.30
431Zadanie 4.32
431Zadanie 4.35
431Zadanie 4.41
432Zadanie 4.42
432
