Wybierz spośród podanych parabolę, która jest symetryczna względem osi y do
![]() .
.
A.
![]()
B.
![]()
C.
![]()
D.
![]()
Wierzchołek paraboli:
![]()
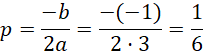
![]()
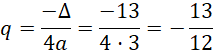
Zatem:
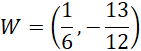
Wierzchołek paraboli odbity względem osi y:
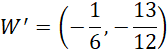
Zatem równanie odbitej paraboli:
![]()
Zatem:
Odp.: A.
![]()

Najpierw wyznacz wierzchołek podanej paraboli. Skorzystaj z zależności, że dla funkcji kwadratowej w postaci ogólnej
![]() parabola ma wierzchołek w punkcie
parabola ma wierzchołek w punkcie
![]() . Współrzędne p i q możemy wyznaczyć ze wzorów:
. Współrzędne p i q możemy wyznaczyć ze wzorów:
![]() oraz
oraz
![]() , gdzie
, gdzie
![]() to tak zwany wyróżnik funkcji, który możemy obliczyć ze wzoru:
to tak zwany wyróżnik funkcji, który możemy obliczyć ze wzoru:
![]() . Następnie odbij symetrycznie wierzchołek paraboli względem osi y i zapisz równanie odpitej paraboli w postaci kanonicznej (pamiętaj, że współczynnik a pozostaje taki sam). Następnie zamień to równanie na postać ogólną.
. Następnie odbij symetrycznie wierzchołek paraboli względem osi y i zapisz równanie odpitej paraboli w postaci kanonicznej (pamiętaj, że współczynnik a pozostaje taki sam). Następnie zamień to równanie na postać ogólną.

Zadanie 1.4
407Zadanie 1.5
407Zadanie 1.6
407Zadanie 1.7
407Zadanie 1.8
408Zadanie 1.10
408Zadanie 1.11
408Zadanie 1.16
409Zadanie 2.4
414Zadanie 2.5
414Zadanie 2.6
414Zadanie 2.7
415Zadanie 2.8
415Zadanie 2.9
415Zadanie 2.10
415Zadanie 2.11
415Zadanie 2.12
415Zadanie 2.13
415Zadanie 2.14
416Zadanie 2.18
416Zadanie 2.19
416Zadanie 2.20
416Zadanie 2.21
416Zadanie 2.22
417Zadanie 2.23
417Zadanie 3.8
423Zadanie 3.9
423Zadanie 3.10
423Zadanie 3.11
423Zadanie 3.12
423Zadanie 3.13
424Zadanie 3.14
424Zadanie 3.15
424Zadanie 3.16
424Zadanie 3.20
424Zadanie 3.23
425Zadanie 3.24
425Zadanie 4.22
430Zadanie 4.23
430Zadanie 4.24
430Zadanie 4.27
431Zadanie 4.30
431Zadanie 4.32
431Zadanie 4.35
431Zadanie 4.41
432Zadanie 4.42
432
