Wyznacz wzór paraboli, której wykres jest symetryczny względem prostej
![]() do paraboli opisanej wzorem:
do paraboli opisanej wzorem:
![]() .
.
Wierzchołek paraboli:
![]()
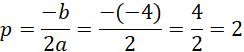
![]()
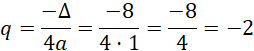
Zatem:
![]()
Postać kanoniczna funkcji:
![]()
Wierzchołek symetryczny względem prostej
![]() do wierzchołka W:
do wierzchołka W:
![]()
Postać kanoniczna funkcji odbitej symetrycznie:
![]()
Postać ogólna:
![]()

Najpierw wyznacz wierzchołek podanej paraboli, aby określić, jak wygląda jej postać kanoniczna. Skorzystaj z zależności, że dla funkcji kwadratowej w postaci ogólnej
![]() parabola ma wierzchołek w punkcie
parabola ma wierzchołek w punkcie
![]() . Współrzędne p i q możemy wyznaczyć ze wzorów:
. Współrzędne p i q możemy wyznaczyć ze wzorów:
![]() oraz
oraz
![]() , gdzie
, gdzie
![]() to tak zwany wyróżnik funkcji, który możemy obliczyć ze wzoru:
to tak zwany wyróżnik funkcji, który możemy obliczyć ze wzoru:
![]() . Następnie odbij wierzchołek paraboli symetrycznie względem podanej prostej. Zrealizuj to za pomocą wzoru
. Następnie odbij wierzchołek paraboli symetrycznie względem podanej prostej. Zrealizuj to za pomocą wzoru
![]() , gdzie n pochodzi z wzoru prostej
, gdzie n pochodzi z wzoru prostej
![]() . Dla odbitego wierzchołka wyznacz wzór kanoniczny nowej paraboli i przekształć ją do postaci ogólnej.
. Dla odbitego wierzchołka wyznacz wzór kanoniczny nowej paraboli i przekształć ją do postaci ogólnej.

Zadanie 1.4
407Zadanie 1.5
407Zadanie 1.6
407Zadanie 1.7
407Zadanie 1.8
408Zadanie 1.10
408Zadanie 1.11
408Zadanie 1.16
409Zadanie 2.4
414Zadanie 2.5
414Zadanie 2.6
414Zadanie 2.7
415Zadanie 2.8
415Zadanie 2.9
415Zadanie 2.10
415Zadanie 2.11
415Zadanie 2.12
415Zadanie 2.13
415Zadanie 2.14
416Zadanie 2.18
416Zadanie 2.19
416Zadanie 2.20
416Zadanie 2.21
416Zadanie 2.22
417Zadanie 2.23
417Zadanie 3.8
423Zadanie 3.9
423Zadanie 3.10
423Zadanie 3.11
423Zadanie 3.12
423Zadanie 3.13
424Zadanie 3.14
424Zadanie 3.15
424Zadanie 3.16
424Zadanie 3.20
424Zadanie 3.23
425Zadanie 3.24
425Zadanie 4.22
430Zadanie 4.23
430Zadanie 4.24
430Zadanie 4.27
431Zadanie 4.30
431Zadanie 4.32
431Zadanie 4.35
431Zadanie 4.41
432Zadanie 4.42
432
