Pewna funkcja kwadratowa
![]() . Wiemy, że
. Wiemy, że
![]() i
i
![]() . Wyznacz wzór tej funkcji.
. Wyznacz wzór tej funkcji.
Szukana funkcja w postaci kanonicznej:
![]()
Skoro
![]() , to wiemy, że oś symetrii paraboli (czyli również pierwsza współrzędna wierzchołka paraboli) leży idealnie pomiędzy argumentami -2019 i 2021. Wyznaczymy tą współrzędną ze średniej arytmetycznej tych dwóch argumentów.
, to wiemy, że oś symetrii paraboli (czyli również pierwsza współrzędna wierzchołka paraboli) leży idealnie pomiędzy argumentami -2019 i 2021. Wyznaczymy tą współrzędną ze średniej arytmetycznej tych dwóch argumentów.
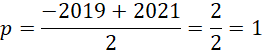
Zatem:
![]()
Skorzystamy teraz z informacji, że
![]() oraz
oraz
![]() i wyznaczymy układ równań:
i wyznaczymy układ równań:
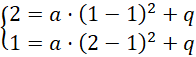
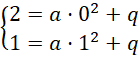
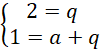
Podstawiamy
![]() do drugiego równania:
do drugiego równania:
![]()
![]()
Zatem:
![]()
Zamieńmy równanie funkcji na postać ogólną:
![]()

Najpierw wyznacz podaną funkcję w postaci kanonicznej
![]() . Następnie wyznacz wartość p korzystając z informacji, że
. Następnie wyznacz wartość p korzystając z informacji, że
![]() – współrzędna p jest idealnie pomiędzy argumentami -2019 i 2021. Następnie utwórz układ równań ze zmiennymi a i q, korzystając z informacji, że
– współrzędna p jest idealnie pomiędzy argumentami -2019 i 2021. Następnie utwórz układ równań ze zmiennymi a i q, korzystając z informacji, że
![]() oraz
oraz
![]() . Rozwiąż układ równań i podstaw wyliczone a i q, do równania w postaci kanonicznej. Następnie zamień to równanie na postać ogólną.
. Rozwiąż układ równań i podstaw wyliczone a i q, do równania w postaci kanonicznej. Następnie zamień to równanie na postać ogólną.

Zadanie 1.4
407Zadanie 1.5
407Zadanie 1.6
407Zadanie 1.7
407Zadanie 1.8
408Zadanie 1.10
408Zadanie 1.11
408Zadanie 1.16
409Zadanie 2.4
414Zadanie 2.5
414Zadanie 2.6
414Zadanie 2.7
415Zadanie 2.8
415Zadanie 2.9
415Zadanie 2.10
415Zadanie 2.11
415Zadanie 2.12
415Zadanie 2.13
415Zadanie 2.14
416Zadanie 2.18
416Zadanie 2.19
416Zadanie 2.20
416Zadanie 2.21
416Zadanie 2.22
417Zadanie 2.23
417Zadanie 3.8
423Zadanie 3.9
423Zadanie 3.10
423Zadanie 3.11
423Zadanie 3.12
423Zadanie 3.13
424Zadanie 3.14
424Zadanie 3.15
424Zadanie 3.16
424Zadanie 3.20
424Zadanie 3.23
425Zadanie 3.24
425Zadanie 4.22
430Zadanie 4.23
430Zadanie 4.24
430Zadanie 4.27
431Zadanie 4.30
431Zadanie 4.32
431Zadanie 4.35
431Zadanie 4.41
432Zadanie 4.42
432
