Pewna funkcja kwadratowa
![]() jest opisana na dziedzinie
jest opisana na dziedzinie
![]() . Jej wykresem jest część paraboli o wierzchołku
. Jej wykresem jest część paraboli o wierzchołku
![]() , która przechodzi przez punkt o współrzędnych
, która przechodzi przez punkt o współrzędnych
![]() . Wyznacz wzór tej funkcji w postaci kanonicznej. Sporządź wykres tej funkcji i podaj jej zbiór wartości.
. Wyznacz wzór tej funkcji w postaci kanonicznej. Sporządź wykres tej funkcji i podaj jej zbiór wartości.
Szukana parabola w postaci kanonicznej.
![]()
Skoro ma wierzchołek w punkcie
![]() , to:
, to:
![]()
![]()
![]()
Wiemy, że parabola przechodzi przez punkt
![]() , zatem:
, zatem:
![]()
![]()
![]()
![]()
Zatem:
![]()
Jest to parabola
![]() przesunięta o wektor
przesunięta o wektor
![]() :
:
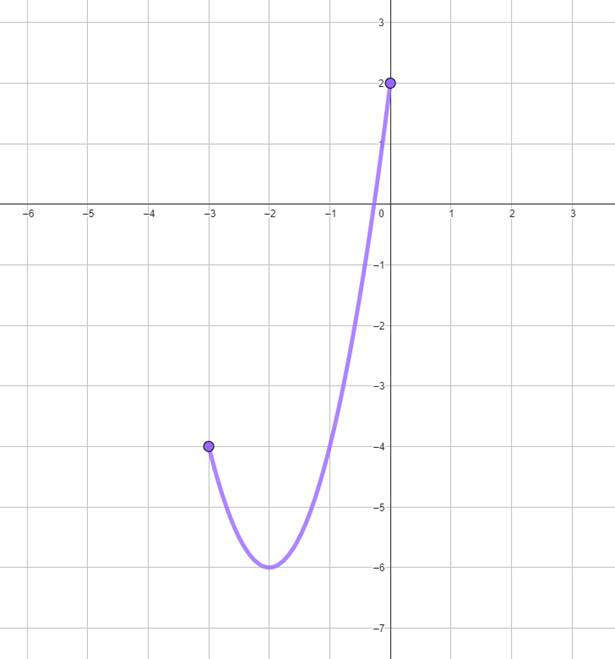
Zbiór wartości:
![]()

Najpierw podstaw współrzędne wierzchołka
![]() do równania paraboli w postaci kanonicznej
do równania paraboli w postaci kanonicznej
![]() . Następnie podstaw współrzędne punku
. Następnie podstaw współrzędne punku
![]() do wzoru paraboli i rozwiąż równanie, aby wyznaczyć wartość współczynnika a. Kiedy wyznaczysz wzór funkcji, narysuj jej wykres na sprecyzowanej dziedzinie. Dla ułatwienia rysowania zauważ, że wyznaczona parabola jest tożsama z funkcją
do wzoru paraboli i rozwiąż równanie, aby wyznaczyć wartość współczynnika a. Kiedy wyznaczysz wzór funkcji, narysuj jej wykres na sprecyzowanej dziedzinie. Dla ułatwienia rysowania zauważ, że wyznaczona parabola jest tożsama z funkcją
![]() przesuniętą o wektor
przesuniętą o wektor
![]() . Na koniec skorzystaj z rysunku, aby wyznaczyć zbiór wartości tej paraboli.
. Na koniec skorzystaj z rysunku, aby wyznaczyć zbiór wartości tej paraboli.

Zadanie 1.4
407Zadanie 1.5
407Zadanie 1.6
407Zadanie 1.7
407Zadanie 1.8
408Zadanie 1.10
408Zadanie 1.11
408Zadanie 1.16
409Zadanie 2.4
414Zadanie 2.5
414Zadanie 2.6
414Zadanie 2.7
415Zadanie 2.8
415Zadanie 2.9
415Zadanie 2.10
415Zadanie 2.11
415Zadanie 2.12
415Zadanie 2.13
415Zadanie 2.14
416Zadanie 2.18
416Zadanie 2.19
416Zadanie 2.20
416Zadanie 2.21
416Zadanie 2.22
417Zadanie 2.23
417Zadanie 3.8
423Zadanie 3.9
423Zadanie 3.10
423Zadanie 3.11
423Zadanie 3.12
423Zadanie 3.13
424Zadanie 3.14
424Zadanie 3.15
424Zadanie 3.16
424Zadanie 3.20
424Zadanie 3.23
425Zadanie 3.24
425Zadanie 4.22
430Zadanie 4.23
430Zadanie 4.24
430Zadanie 4.27
431Zadanie 4.30
431Zadanie 4.32
431Zadanie 4.35
431Zadanie 4.41
432Zadanie 4.42
432
