Wiemy, że wykres paraboli ma wierzchołek w punkcie
![]() oraz że przechodzi przez punkt
oraz że przechodzi przez punkt
![]() . Wyznacz wzór tej paraboli w postaci kanonicznej.
. Wyznacz wzór tej paraboli w postaci kanonicznej.
Szukana funkcja kwadratowa:
![]()
Skoro wykres paraboli ma wierzchołek w punkcie
![]() , to:
, to:
![]()
![]()
![]()
Skoro parabola przechodzi przez punkt
![]() , to:
, to:
![]()
![]()
![]()
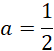
Zatem:
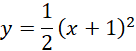

Najpierw wyznacz wartości p i q we wzorze paraboli, korzystając z tego, że dla paraboli o równaniu w postaci kanonicznej
![]() wierzchołek znajduje się w punkcie
wierzchołek znajduje się w punkcie
![]() . Następnie oblicz wartość współczynnika a poprzez podstawienie współrzędnych punktu P do wzoru paraboli i rozwiąż równanie.
. Następnie oblicz wartość współczynnika a poprzez podstawienie współrzędnych punktu P do wzoru paraboli i rozwiąż równanie.

Zadanie 1.4
407Zadanie 1.5
407Zadanie 1.6
407Zadanie 1.7
407Zadanie 1.8
408Zadanie 1.10
408Zadanie 1.11
408Zadanie 1.16
409Zadanie 2.4
414Zadanie 2.5
414Zadanie 2.6
414Zadanie 2.7
415Zadanie 2.8
415Zadanie 2.9
415Zadanie 2.10
415Zadanie 2.11
415Zadanie 2.12
415Zadanie 2.13
415Zadanie 2.14
416Zadanie 2.18
416Zadanie 2.19
416Zadanie 2.20
416Zadanie 2.21
416Zadanie 2.22
417Zadanie 2.23
417Zadanie 3.8
423Zadanie 3.9
423Zadanie 3.10
423Zadanie 3.11
423Zadanie 3.12
423Zadanie 3.13
424Zadanie 3.14
424Zadanie 3.15
424Zadanie 3.16
424Zadanie 3.20
424Zadanie 3.23
425Zadanie 3.24
425Zadanie 4.22
430Zadanie 4.23
430Zadanie 4.24
430Zadanie 4.27
431Zadanie 4.30
431Zadanie 4.32
431Zadanie 4.35
431Zadanie 4.41
432Zadanie 4.42
432
