Mamy podane równanie
![]() . Sporządź odpowiedni wykres i korzystając z niego wyznacz liczbę rozwiązań równania w zależności od wartości parametru m.
. Sporządź odpowiedni wykres i korzystając z niego wyznacz liczbę rozwiązań równania w zależności od wartości parametru m.
Krok 1:
![]()
Krok 2:
![]()
Krok 3:
![]()
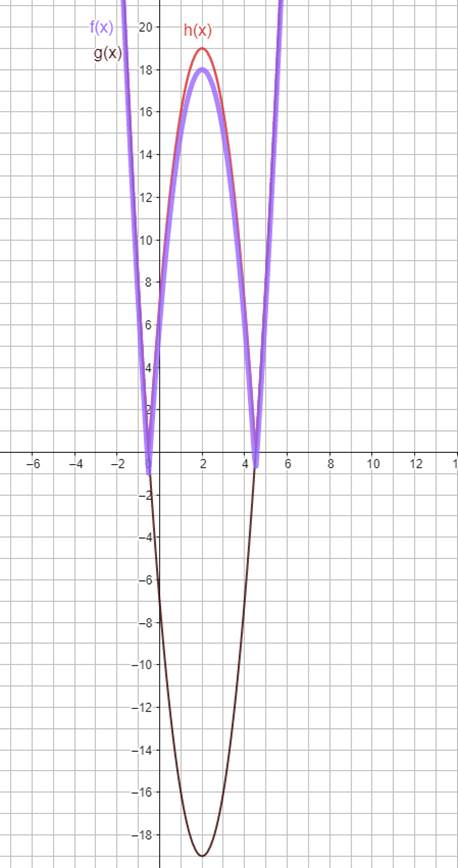
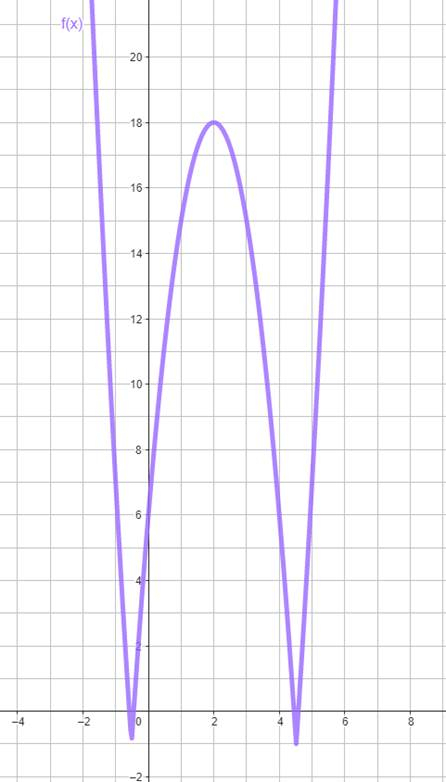
Sama funkcja
![]() :
:
![]() ma zero rozwiązań dla
ma zero rozwiązań dla
![]()
![]() ma dwa rozwiązania dla
ma dwa rozwiązania dla
![]()
![]() ma cztery rozwiązania dla
ma cztery rozwiązania dla
![]()
![]() ma trzy rozwiązania dla
ma trzy rozwiązania dla
![]()

Narysuj funkcję
![]() . Do narysowania podanej funkcji skorzystaj z odpowiednich przekształceń:
. Do narysowania podanej funkcji skorzystaj z odpowiednich przekształceń:
Krok 1: Sprowadź funkcję
![]() do postaci kanonicznej w następujący sposób – najpierw rozbij współczynnik c na takie liczby, aby jedna z nich pasowała do wzoru skróconego mnożenia z
do postaci kanonicznej w następujący sposób – najpierw rozbij współczynnik c na takie liczby, aby jedna z nich pasowała do wzoru skróconego mnożenia z
![]() i
i
![]() (musi pasować po wyciągnięciu współczynnika a przed nawias). Następnie wyciągnij współczynnik a przed nawias z trzech pierwszych wyrażeń, a na koniec skorzystaj ze wzorów skróconego mnożenia do zwinięcia nawiasu w kwadrat sumy lub kwadrat różnicy. Jak wyznaczysz wzór paraboli w postaci kanonicznej, narysuj jej wykres. Zauważ, że jest to funkcja
(musi pasować po wyciągnięciu współczynnika a przed nawias). Następnie wyciągnij współczynnik a przed nawias z trzech pierwszych wyrażeń, a na koniec skorzystaj ze wzorów skróconego mnożenia do zwinięcia nawiasu w kwadrat sumy lub kwadrat różnicy. Jak wyznaczysz wzór paraboli w postaci kanonicznej, narysuj jej wykres. Zauważ, że jest to funkcja
![]() przesunięta o wektor
przesunięta o wektor
![]() .
.
Krok 2: Obłóż funkcję
![]() wartością bezwzględną. Polega to na odbiciu symetrycznym względem osi x tej części wykresu, która znajduje się pod osią.
wartością bezwzględną. Polega to na odbiciu symetrycznym względem osi x tej części wykresu, która znajduje się pod osią.
Krok 3: Przesuń wykres funkcji
![]() o jedną jednostkę w dół.
o jedną jednostkę w dół.
Następnie wyznacz liczbę rozwiązań równania
![]() w zależności od parametru m. Polega to na znalezieniu to takich przedziałów na osi y, z których wartości są osiągane przez funkcję określoną liczbę razy.
w zależności od parametru m. Polega to na znalezieniu to takich przedziałów na osi y, z których wartości są osiągane przez funkcję określoną liczbę razy.

Zadanie 1.4
407Zadanie 1.5
407Zadanie 1.6
407Zadanie 1.7
407Zadanie 1.8
408Zadanie 1.10
408Zadanie 1.11
408Zadanie 1.16
409Zadanie 2.4
414Zadanie 2.5
414Zadanie 2.6
414Zadanie 2.7
415Zadanie 2.8
415Zadanie 2.9
415Zadanie 2.10
415Zadanie 2.11
415Zadanie 2.12
415Zadanie 2.13
415Zadanie 2.14
416Zadanie 2.18
416Zadanie 2.19
416Zadanie 2.20
416Zadanie 2.21
416Zadanie 2.22
417Zadanie 2.23
417Zadanie 3.8
423Zadanie 3.9
423Zadanie 3.10
423Zadanie 3.11
423Zadanie 3.12
423Zadanie 3.13
424Zadanie 3.14
424Zadanie 3.15
424Zadanie 3.16
424Zadanie 3.20
424Zadanie 3.23
425Zadanie 3.24
425Zadanie 4.22
430Zadanie 4.23
430Zadanie 4.24
430Zadanie 4.27
431Zadanie 4.30
431Zadanie 4.32
431Zadanie 4.35
431Zadanie 4.41
432Zadanie 4.42
432
