Podana jest funkcja
![]() . Oceń, czy podane zdania są prawdziwe czy fałszywe.
. Oceń, czy podane zdania są prawdziwe czy fałszywe.
A. Zbiorem wartości funkcji
![]() jest przedział
jest przedział
![]() .
.
B. Osią symetrii wykresu funkcji
![]() jest prosta
jest prosta
![]() .
.
C. Równanie
![]() ma dwa rozwiązania.
ma dwa rozwiązania.
Wierzchołek paraboli:
![]()
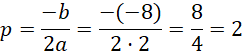
![]()
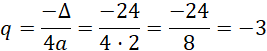
Zatem:
![]()
Skoro
![]() , to parabola ma ramiona skierowane do góry, zatem:
, to parabola ma ramiona skierowane do góry, zatem:
![]()
Zdanie A jest fałszywe.
Prosta
![]() nie przechodzi przez
nie przechodzi przez
![]() , zatem:
, zatem:
Zdanie B jest fałszywe.
-2 jest powyżej -3, a skoro ramiona ma ramiona skierowana w górę, to
![]() ma dwa rozwiązania, zatem:
ma dwa rozwiązania, zatem:
Zdanie C jest prawdziwe.

Najpierw wyznacz wierzchołek paraboli podanej funkcji. Skorzystaj z zależności, że dla funkcji kwadratowej w postaci ogólnej
![]() parabola ma wierzchołek w punkcie
parabola ma wierzchołek w punkcie
![]() . Współrzędne p i q możemy wyznaczyć ze wzorów:
. Współrzędne p i q możemy wyznaczyć ze wzorów:
![]() oraz
oraz
![]() , gdzie
, gdzie
![]() to tak zwany wyróżnik funkcji, który możemy obliczyć ze wzoru:
to tak zwany wyróżnik funkcji, który możemy obliczyć ze wzoru:
![]() . Następnie zauważ, że współczynnik a tej paraboli jest dodatni, zatem parabola ma ramiona skierowane do góry. Skorzystaj z tych spostrzeżeń, aby ocenić prawdziwość podanych zdań.
. Następnie zauważ, że współczynnik a tej paraboli jest dodatni, zatem parabola ma ramiona skierowane do góry. Skorzystaj z tych spostrzeżeń, aby ocenić prawdziwość podanych zdań.

Zadanie 1.4
407Zadanie 1.5
407Zadanie 1.6
407Zadanie 1.7
407Zadanie 1.8
408Zadanie 1.10
408Zadanie 1.11
408Zadanie 1.16
409Zadanie 2.4
414Zadanie 2.5
414Zadanie 2.6
414Zadanie 2.7
415Zadanie 2.8
415Zadanie 2.9
415Zadanie 2.10
415Zadanie 2.11
415Zadanie 2.12
415Zadanie 2.13
415Zadanie 2.14
416Zadanie 2.18
416Zadanie 2.19
416Zadanie 2.20
416Zadanie 2.21
416Zadanie 2.22
417Zadanie 2.23
417Zadanie 3.8
423Zadanie 3.9
423Zadanie 3.10
423Zadanie 3.11
423Zadanie 3.12
423Zadanie 3.13
424Zadanie 3.14
424Zadanie 3.15
424Zadanie 3.16
424Zadanie 3.20
424Zadanie 3.23
425Zadanie 3.24
425Zadanie 4.22
430Zadanie 4.23
430Zadanie 4.24
430Zadanie 4.27
431Zadanie 4.30
431Zadanie 4.32
431Zadanie 4.35
431Zadanie 4.41
432Zadanie 4.42
432
