Podana jest funkcja o równaniu
![]() . Wiemy, że funkcja przyjmuje takie same wartości dla argumentów 1 i 5 oraz że początek układu współrzędnych leży na wykresie tej funkcji. Wyznacz wartości współczynników b i c.
. Wiemy, że funkcja przyjmuje takie same wartości dla argumentów 1 i 5 oraz że początek układu współrzędnych leży na wykresie tej funkcji. Wyznacz wartości współczynników b i c.
Skoro
![]() , oznacza to, że oś symetrii znajduje się po środku pomiędzy argumentami 1 i 5.
, oznacza to, że oś symetrii znajduje się po środku pomiędzy argumentami 1 i 5.
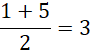
Zatem oś symetrii ma równanie:
![]()
A wierzchołek paraboli ma pierwszą współrzędną równą 3:
![]()
Zatem postać kanoniczna funkcji:
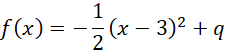
Wiemy, że początek układu współrzędnych (punkt
![]() ) należy do wykresu paraboli, zatem:
) należy do wykresu paraboli, zatem:
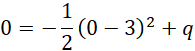
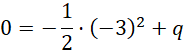
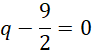
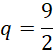
Zatem:
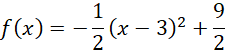
Zamieńmy na postać ogólną:
![]()
Zatem:
![]()
![]()

Zacznij od wyznaczenia pierwszej współrzędnej wierzchołka paraboli, korzystając z informacji, że funkcja przyjmuje jednakowe wartości dla argumentów 1 i 5. Oznacza to, że wierzchołek musi znajdować pośrodku pomiędzy 1 i 5, czyli
![]() . Następnie wyznacz postać kanonicznej podanej funkcji, korzystając z zależności, że parabola o wierzchołku
. Następnie wyznacz postać kanonicznej podanej funkcji, korzystając z zależności, że parabola o wierzchołku
![]() ma postać kanoniczną
ma postać kanoniczną
![]() . Wyznacz wartość q, poprzez podstawienie współrzędnych początku układu współrzędnych do równania i rozwiązanie go. Następnie zamień wyznaczone równanie w postaci kanonicznej na postać ogólną. Zauważ, że możesz odczytać wartości współczynników b i c bezpośrednio z wyznaczonej postaci ogólnej.
. Wyznacz wartość q, poprzez podstawienie współrzędnych początku układu współrzędnych do równania i rozwiązanie go. Następnie zamień wyznaczone równanie w postaci kanonicznej na postać ogólną. Zauważ, że możesz odczytać wartości współczynników b i c bezpośrednio z wyznaczonej postaci ogólnej.

Zadanie 1.4
407Zadanie 1.5
407Zadanie 1.6
407Zadanie 1.7
407Zadanie 1.8
408Zadanie 1.10
408Zadanie 1.11
408Zadanie 1.16
409Zadanie 2.4
414Zadanie 2.5
414Zadanie 2.6
414Zadanie 2.7
415Zadanie 2.8
415Zadanie 2.9
415Zadanie 2.10
415Zadanie 2.11
415Zadanie 2.12
415Zadanie 2.13
415Zadanie 2.14
416Zadanie 2.18
416Zadanie 2.19
416Zadanie 2.20
416Zadanie 2.21
416Zadanie 2.22
417Zadanie 2.23
417Zadanie 3.8
423Zadanie 3.9
423Zadanie 3.10
423Zadanie 3.11
423Zadanie 3.12
423Zadanie 3.13
424Zadanie 3.14
424Zadanie 3.15
424Zadanie 3.16
424Zadanie 3.20
424Zadanie 3.23
425Zadanie 3.24
425Zadanie 4.22
430Zadanie 4.23
430Zadanie 4.24
430Zadanie 4.27
431Zadanie 4.30
431Zadanie 4.32
431Zadanie 4.35
431Zadanie 4.41
432Zadanie 4.42
432
