Musisz wyprowadzić wzór na zadaną długość odcinka za pomocą twierdzenia Talesa.
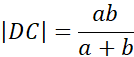

Sytuacja przedstawiona na rysunku:
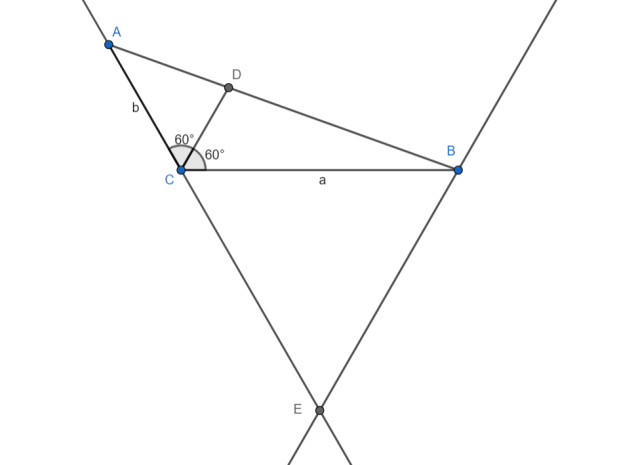
Poprowadźmy z punktu B prostą równoległą do odcinka |CD|. Oraz prostą która zawiera odcinek |AC|. Punkt ich przecięcia oznaczmy literą E.
Możemy teraz wywnioskować, że:
![]()
A także, że kąty DCA oraz BEC są sobie równe (kąty odpowiadające):
![]()
Możemy więc zauważyć, że pozostały kąt CBE wynosi:
![]()
A trójkąt BCE jest trójkątem równobocznym z cechy kąt-kąt-kat, więc:
![]()
Następnie wiedząc, że odcinki |CD| i |BE| są względem siebie równoległe możemy zapisać twierdzenie Talesa:
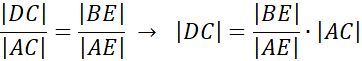
Podstawiając znane wartości:
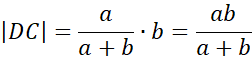

Zadanie 1.1.
146Zadanie 1.4.
147Zadanie 1.8.
147Zadanie 1.13.
147Zadanie 1.18.
148Zadanie 1.19.
148Zadanie 1.24.
148Zadanie 1.27.
148Zadanie 2.1.
159Zadanie 2.2.
159Zadanie 2.7.
159Zadanie 2.12.
148Zadanie 3.3.
174Zadanie 3.12.
175Zadanie 3.13.
175Zadanie 3.15.
176Zadanie 4.2.
183Zadanie 4.3.
184Zadanie 4.4.
184Zadanie 4.6.
184Zadanie 4.7.
184Zadanie 4.8.
184Zadanie 4.9.
184Zadanie Prosto do matury 5.
186Zadanie 5.2.
192Zadanie 5.3.
192Zadanie 5.6.
193Zadanie 5.7.
193Zadanie 5.9.
193Zadanie 6.2.
208Zadanie 6.3.
209Zadanie 6.4.
209Zadanie 6.5.
209Zadanie 6.10.
210Zadanie 30.
217Zadanie 39.
218
