Musisz wyznaczyć wartość zadanego kąta na podstawie znanych zależności.
![]()

Spójrzmy na sytuację przedstawioną na rysunku:
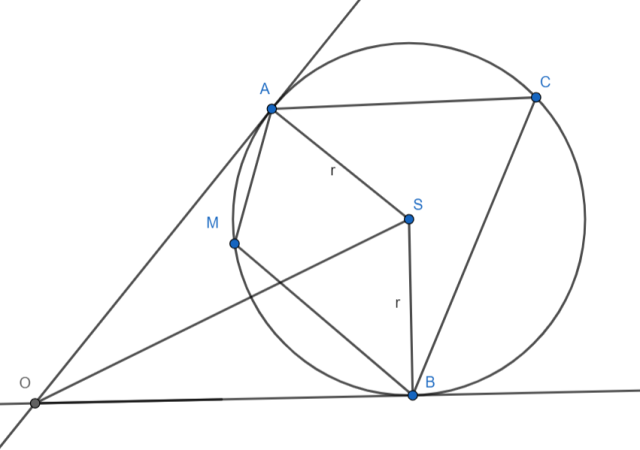
Do sytuacji opisanej w poleceniu dodaliśmy:
O – punkt w kącie α = 50°
S – punkt w środku koła
C – dowolny punkt na dłuższym łuku AB
Analizując rysunek, wiemy, że:
Kąty ∠OAS i ∠OBS są kątami prostymi (ponieważ odcinki |OA| i |OB| leżą na stycznych do okręgu).
![]()
Kąty ∠AOS i ∠BOS są sobie równe:
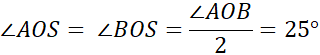
Tak więc:
![]()
Kąt ∠ACB jest kątem wpisanym na tym samym łuku co kąt środkowy ∠ASB więc:
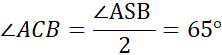
Ostatecznie z twierdzenia o kątach przeciwległych w czworokątach wpisanych w okrąg:
![]()

Zadanie 1.1.
146Zadanie 1.4.
147Zadanie 1.8.
147Zadanie 1.13.
147Zadanie 1.18.
148Zadanie 1.19.
148Zadanie 1.24.
148Zadanie 1.27.
148Zadanie 2.1.
159Zadanie 2.2.
159Zadanie 2.7.
159Zadanie 2.12.
148Zadanie 3.3.
174Zadanie 3.12.
175Zadanie 3.13.
175Zadanie 3.15.
176Zadanie 4.2.
183Zadanie 4.3.
184Zadanie 4.4.
184Zadanie 4.6.
184Zadanie 4.7.
184Zadanie 4.8.
184Zadanie 4.9.
184Zadanie Prosto do matury 5.
186Zadanie 5.2.
192Zadanie 5.3.
192Zadanie 5.6.
193Zadanie 5.7.
193Zadanie 5.9.
193Zadanie 6.2.
208Zadanie 6.3.
209Zadanie 6.4.
209Zadanie 6.5.
209Zadanie 6.10.
210Zadanie 30.
217Zadanie 39.
218
