Musisz przeanalizować podane figury oraz ocenić ich podobieństwo.
Tak w skali k = 3.

Wyznaczmy wartości w obu trójkątach, które jednoznacznie pozwolą nam ocenić, czy są one podobne:
Trójkąt równoramienny o ramieniu 30 cm i wysokości opuszczonej na podstawę równej 24 cm przyjmijmy za trójkąt nr 2. Z opisu możemy obliczyć długość połowy podstawy trójkąta równoramiennego za pomocą twierdzenia Pitagorasa:
Niech: a2 - długość połowy podstawy trójkąta równoramiennego nr 2
![]()
W takim razie podstawa tego trójkąta wynosi:
![]()
Sprawdźmy teraz czy stosunek ramienia do podstawy w obu trójkątach jest równy:
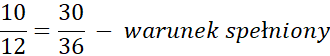
Skala k wynosi:
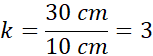

Zadanie 1.1.
146Zadanie 1.4.
147Zadanie 1.8.
147Zadanie 1.13.
147Zadanie 1.18.
148Zadanie 1.19.
148Zadanie 1.24.
148Zadanie 1.27.
148Zadanie 2.1.
159Zadanie 2.2.
159Zadanie 2.7.
159Zadanie 2.12.
148Zadanie 3.3.
174Zadanie 3.12.
175Zadanie 3.13.
175Zadanie 3.15.
176Zadanie 4.2.
183Zadanie 4.3.
184Zadanie 4.4.
184Zadanie 4.6.
184Zadanie 4.7.
184Zadanie 4.8.
184Zadanie 4.9.
184Zadanie Prosto do matury 5.
186Zadanie 5.2.
192Zadanie 5.3.
192Zadanie 5.6.
193Zadanie 5.7.
193Zadanie 5.9.
193Zadanie 6.2.
208Zadanie 6.3.
209Zadanie 6.4.
209Zadanie 6.5.
209Zadanie 6.10.
210Zadanie 30.
217Zadanie 39.
218
