Musisz narysować zadany trójkąt oraz opisać na nim okrąg.

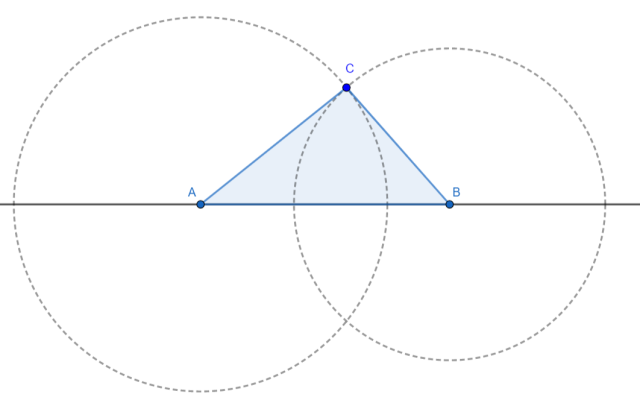
Instrukcja konstrukcji zadanego trójkąta:
1. Narysuj dowolną prostą.
2. Odmierz cyrklem 8cm. Narysuj na prostej odcinek AB o długości 8 cm.
3. Odmierz cyrklem 6cm. Narysuj okrąg z punktu A.
4. Odmierz cyrklem 5cm. Narysuj okrąg z punktu B.
5. Punkt przecięcia okręgów z punktu 3 i 4 to pozostały wierzchołek trójkąta. Oznacz go literą C.
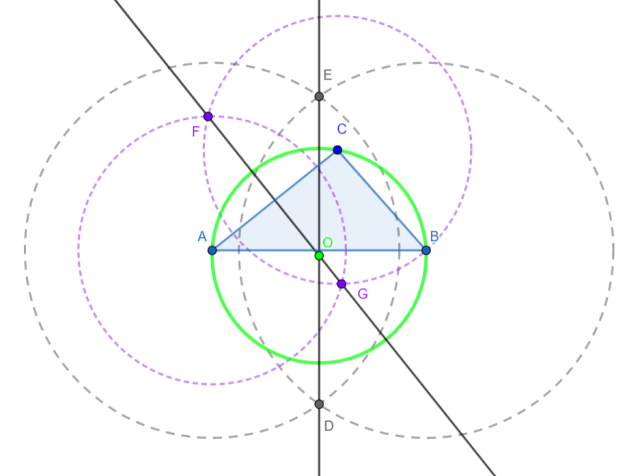
Instrukcja okręgu opisanego:
1. Odmierz cyrklem odcinek dłuższy niż połowa AB Z punktów A i B narysuj okręgi. Punkty przecięcia się okręgów nazwij E i D. Poprowadź prostą (symetralną) przez punkty E i D.
2. Odmierz cyrklem odcinek dłuższy niż połowa AC Z punktów A i C narysuj okręgi. Punkty przecięcia się okręgów nazwij F i G. Poprowadź prostą (symetralną) przez punkty F i G.
3. Oznacz punkt przecięcia się prostych z punktu 1 i 2 literą O. To środek szukanego okręgu.
4. Odmierz cyrklem odcinek OA. Narysuj okrąg o środku O – to twój zadany okrąg.

Zadanie 1.1.
146Zadanie 1.4.
147Zadanie 1.8.
147Zadanie 1.13.
147Zadanie 1.18.
148Zadanie 1.19.
148Zadanie 1.24.
148Zadanie 1.27.
148Zadanie 2.1.
159Zadanie 2.2.
159Zadanie 2.7.
159Zadanie 2.12.
148Zadanie 3.3.
174Zadanie 3.12.
175Zadanie 3.13.
175Zadanie 3.15.
176Zadanie 4.2.
183Zadanie 4.3.
184Zadanie 4.4.
184Zadanie 4.6.
184Zadanie 4.7.
184Zadanie 4.8.
184Zadanie 4.9.
184Zadanie Prosto do matury 5.
186Zadanie 5.2.
192Zadanie 5.3.
192Zadanie 5.6.
193Zadanie 5.7.
193Zadanie 5.9.
193Zadanie 6.2.
208Zadanie 6.3.
209Zadanie 6.4.
209Zadanie 6.5.
209Zadanie 6.10.
210Zadanie 30.
217Zadanie 39.
218
