Musisz obliczyć długość zadanego odcinka.
![]()

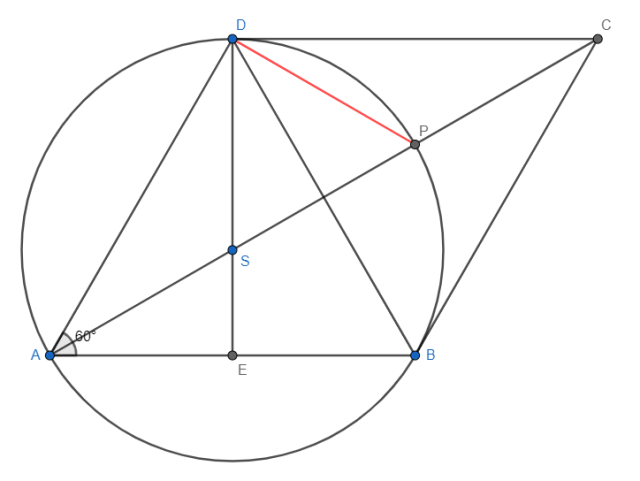
Przyjmując oznaczenia zgodnie z rysunkiem powyżej, możemy zauważyć, że:
![]()
![]()
Można więc zauważyć, że:
![]()
Kąty DSP i ASE są kątami wierzchołkowymi, więc:
![]()
Trójkąt ASD jest trójkątem równoramiennym o ramieniu równym promieniowi okręgu, więc:
![]()
Jeden z boków trójkąta ADP jest średnicą okręgu, więc:
![]()
Możemy zauważyć:
![]()
![]()
Można zauważyć, że środek okręgu S dzieli wysokość trójkąta ABD w stosunku 2:1, a promień okręgu możemy wyznaczyć:
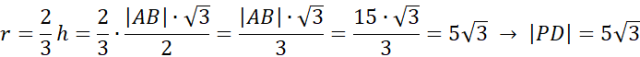

Zadanie 1.1.
146Zadanie 1.4.
147Zadanie 1.8.
147Zadanie 1.13.
147Zadanie 1.18.
148Zadanie 1.19.
148Zadanie 1.24.
148Zadanie 1.27.
148Zadanie 2.1.
159Zadanie 2.2.
159Zadanie 2.7.
159Zadanie 2.12.
148Zadanie 3.3.
174Zadanie 3.12.
175Zadanie 3.13.
175Zadanie 3.15.
176Zadanie 4.2.
183Zadanie 4.3.
184Zadanie 4.4.
184Zadanie 4.6.
184Zadanie 4.7.
184Zadanie 4.8.
184Zadanie 4.9.
184Zadanie Prosto do matury 5.
186Zadanie 5.2.
192Zadanie 5.3.
192Zadanie 5.6.
193Zadanie 5.7.
193Zadanie 5.9.
193Zadanie 6.2.
208Zadanie 6.3.
209Zadanie 6.4.
209Zadanie 6.5.
209Zadanie 6.10.
210Zadanie 30.
217Zadanie 39.
218
