Udowodnij, że styczne poprowadzone do okręgów odpowiednio w punktach A i B są równoległe, wiedząc, że przez punkt styczności M dwóch okręgów poprowadzona została prosta przecinająca je w punktach A i B
Sytuacja przedstawiona na rysunku:
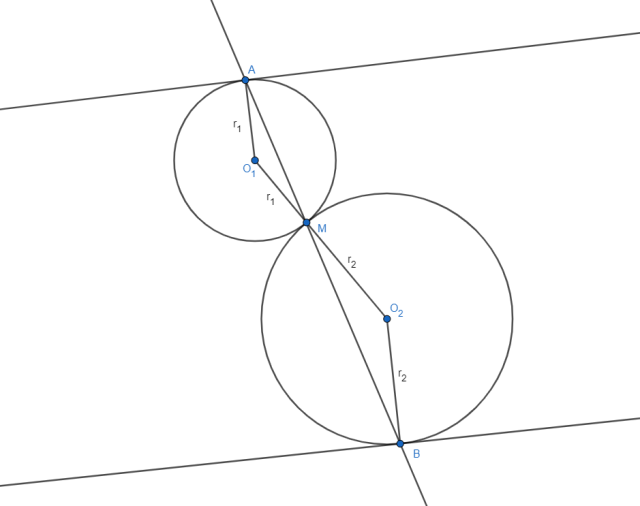
Trójkąty BO2M i AO1M są trójkątami równoramiennymi o ramionach równym odpowiednim promieniom okręgów, więc:
![]()
![]()
Poza tym kąty ∠AMO1 i ∠BMO2są kątami wierzchołkowymi więc:
![]()
Stąd możemy stwierdzić, że ostre kąty przecięcia się prostej |AB| z obiema stycznymi są ze sobą równe:
![]()
Co oznacza, że są to kąty naprzemianległe pomiędzy dwoma równoległymi prostymi (stycznymi w punktach A i B). - c. n. d.


Zadanie 1.1.
146Zadanie 1.4.
147Zadanie 1.8.
147Zadanie 1.13.
147Zadanie 1.18.
148Zadanie 1.19.
148Zadanie 1.24.
148Zadanie 1.27.
148Zadanie 2.1.
159Zadanie 2.2.
159Zadanie 2.7.
159Zadanie 2.12.
148Zadanie 3.3.
174Zadanie 3.12.
175Zadanie 3.13.
175Zadanie 3.15.
176Zadanie 4.2.
183Zadanie 4.3.
184Zadanie 4.4.
184Zadanie 4.6.
184Zadanie 4.7.
184Zadanie 4.8.
184Zadanie 4.9.
184Zadanie Prosto do matury 5.
186Zadanie 5.2.
192Zadanie 5.3.
192Zadanie 5.6.
193Zadanie 5.7.
193Zadanie 5.9.
193Zadanie 6.2.
208Zadanie 6.3.
209Zadanie 6.4.
209Zadanie 6.5.
209Zadanie 6.10.
210Zadanie 30.
217Zadanie 39.
218
