Musisz udowodnić podany wzór.
Podzielmy n –kąt na trójkąty prowadząc wszystkie przekątne z jednego ustalonego wierzchołka.
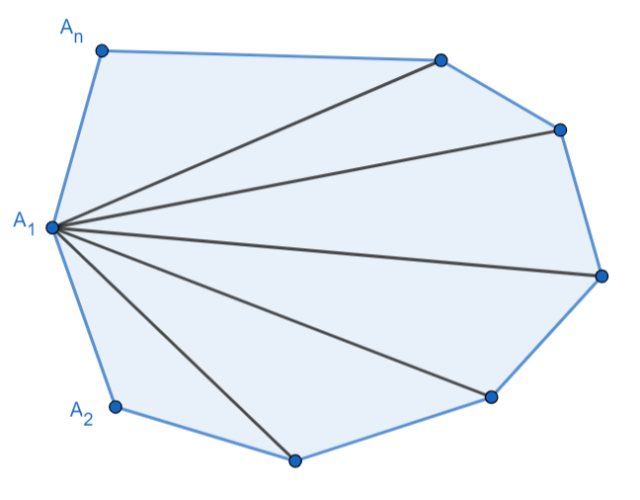
Ponieważ z wierzchołka wychodzi n−3 przekątnych (nie uwzględnia się wierzchołka A1 oraz sąsiadujących A2 i An), więc otrzymamy n−2 trójkątów. Wzór na sumę kątów tych trójkątów to dokładnie suma kątów wewnętrznych n –kąta, co daje nam żądaną równość:
![]()


Zadanie 1.1.
146Zadanie 1.4.
147Zadanie 1.8.
147Zadanie 1.13.
147Zadanie 1.18.
148Zadanie 1.19.
148Zadanie 1.24.
148Zadanie 1.27.
148Zadanie 2.1.
159Zadanie 2.2.
159Zadanie 2.7.
159Zadanie 2.12.
148Zadanie 3.3.
174Zadanie 3.12.
175Zadanie 3.13.
175Zadanie 3.15.
176Zadanie 4.2.
183Zadanie 4.3.
184Zadanie 4.4.
184Zadanie 4.6.
184Zadanie 4.7.
184Zadanie 4.8.
184Zadanie 4.9.
184Zadanie Prosto do matury 5.
186Zadanie 5.2.
192Zadanie 5.3.
192Zadanie 5.6.
193Zadanie 5.7.
193Zadanie 5.9.
193Zadanie 6.2.
208Zadanie 6.3.
209Zadanie 6.4.
209Zadanie 6.5.
209Zadanie 6.10.
210Zadanie 30.
217Zadanie 39.
218
