Musisz udowodnić równość podanych kątów w trójkącie.
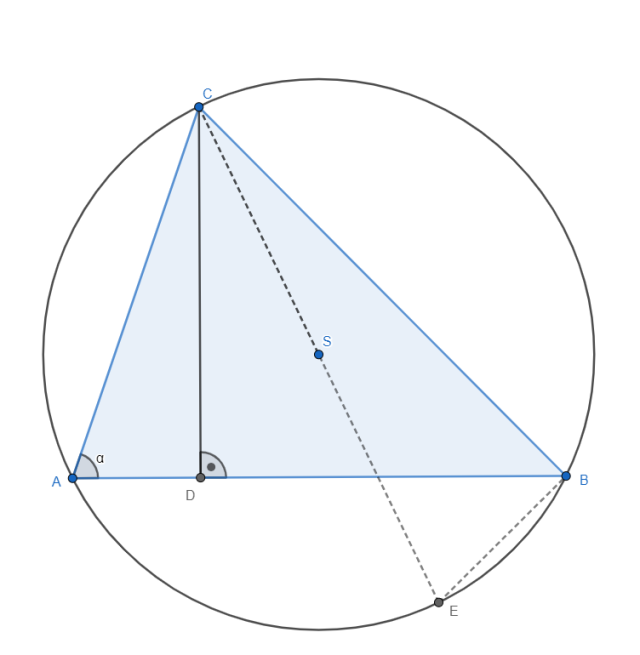
Przyjmując oznaczenia zgodnie z rysunkiem powyżej, załóżmy:
![]()
Poprowadźmy średnicę okręgu z punktu C do punku E. Zauważmy, że wtedy jeden z boków trójkąta BCE jest średnicą okręgu, a to oznacza, że:
![]()
Zauważmy również, że kąty CAB i CEB są kątami wpisanymi leżącymi na tym samym łuku BC. Oznacza to, że są one sobie równe:
![]()
Z zależności kątów w trójkącie CAD:
![]()
Z zależności kątów w trójkącie CBE:
![]()
Podsumowując:
![]()


Zadanie 1.1.
146Zadanie 1.4.
147Zadanie 1.8.
147Zadanie 1.13.
147Zadanie 1.18.
148Zadanie 1.19.
148Zadanie 1.24.
148Zadanie 1.27.
148Zadanie 2.1.
159Zadanie 2.2.
159Zadanie 2.7.
159Zadanie 2.12.
148Zadanie 3.3.
174Zadanie 3.12.
175Zadanie 3.13.
175Zadanie 3.15.
176Zadanie 4.2.
183Zadanie 4.3.
184Zadanie 4.4.
184Zadanie 4.6.
184Zadanie 4.7.
184Zadanie 4.8.
184Zadanie 4.9.
184Zadanie Prosto do matury 5.
186Zadanie 5.2.
192Zadanie 5.3.
192Zadanie 5.6.
193Zadanie 5.7.
193Zadanie 5.9.
193Zadanie 6.2.
208Zadanie 6.3.
209Zadanie 6.4.
209Zadanie 6.5.
209Zadanie 6.10.
210Zadanie 30.
217Zadanie 39.
218
