Wykaż, że czworokąt A’B’C’D’ jest prostokątem o polu dwa razy mniejszym od pola rombu, jeśli w rombie ABCD połączono środki kolejnych boków i otrzymano czworokąt A’B’C’D’.

Przeciwległe kąty w równoległoboku mają takie same miary, a suma miar kątów znajdujących się przy jednym boku wynosi $\text{[math]}$ , więc:

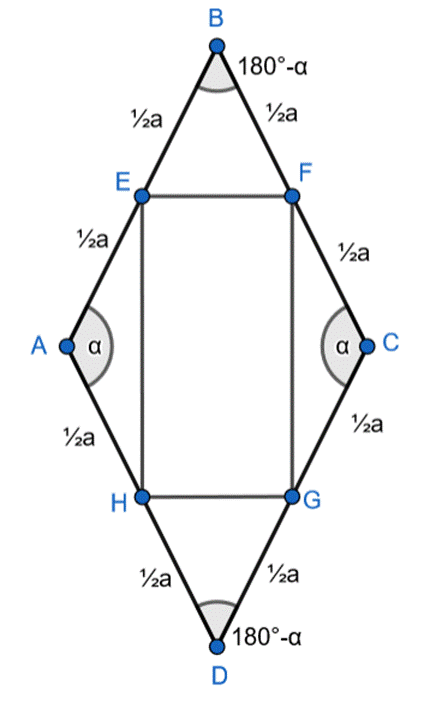
Oznacza to, że trójkąty AEH i FCG oraz EBF i GDH są przystające z cechy BKB: $\text{[math]}$ .

Więc odpowiadające sobie boki w każdej parze trójkątów mają takie same długości:

$\text{[math]}$

Trójkąty AEH, FCG, EBF i GDH są równoramienne, więc ich kąty przy podstawie mają takie same miary. Korzystając z tego, że suma miar kątów w trójkącie wynosi $\text{[math]}$ otrzymujemy:

$\text{[math]}$

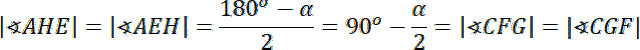
Kąty AEH, HEF, BEF i BFE, EFG, GFC i CGF, FGH, HGD oraz DHG, GHE, AHE tworzą kąty przyległe, których suma miar wynosi $\text{[math]}$ , więc:

$\text{[math]}$

Oznacza to, że czworokąt EFGH ma dwie pary równoległych boków i wszystkie kąty proste, więc jest prostokątem.

To kończy dowód.

Zadanie 4., strona 68, Matematyka z kluczem. Klasa 6. Zeszyt ćwiczeń – rozwiązania i odpowiedzi

Zadanie sprawdź, czy umiesz 1, strona 231, Matematyka z plusem. Klasa 7. Podręcznik – rozwiązania i odpowiedzi

Zadanie 1., strona 70, Matematyka z plusem. Klasa 5. Zeszyt ćwiczeń. Wersja A. Część 3/3 – rozwiązania i odpowiedzi

Zadanie zamknięte 4, strona 121, Matematyka wokół nas. Klasa 5. Zbiór zadań – rozwiązania i odpowiedzi

Zadanie 8, strona 49, MATeMAtyka 1. Karty pracy ucznia. Zakres podstawowy

Ćwiczenie 57., strona 52, Matematyka z plusem. Klasa 5. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie 8., strona 231, Matematyka. Klasa 1. Podręcznik. Zakres podstawowy - rozwiązania i odpowiedzi

Zadanie 26, strona 22, Matematyka z plusem. Klasa 6. Zbiór zadań – rozwiązania i odpowiedzi

Ćwiczenie 3, strona 34, Matematyka. Klasa 6. Podręcznik - rozwiązania i odpowiedzi

Zadanie 11, strona 84, Matematyka wokół nas. Klasa 6. Podręcznik – rozwiązania i odpowiedzi

Zadanie 1

242

NOWA MATeMAtyka. Klasa 1. Zakres podstawowy - rozwiązania i odpowiedzi

Zadanie 5 - strona 274

Zadanie

Wykaż, że czworokąt A’B’C’D’ jest prostokątem o polu dwa razy mniejszym od pola rombu, jeśli w rombie ABCD połączono środki kolejnych boków i otrzymano czworokąt A’B’C’D’.

Rozwiązanie

Matematyka - wybrane pytania