Wyznacz długość odcinka PQ i pole trójkąta CPQ, jeśli w trójkącie ABC o polu
bok AB ma długość 20 dm, punkt P leży na boku AC i
oraz punkt Q leży na boku BC i
.
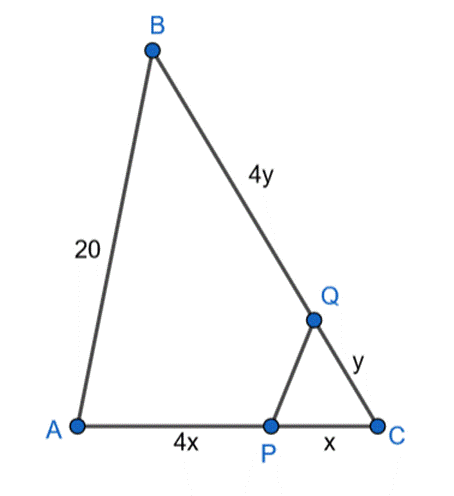
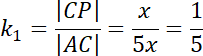
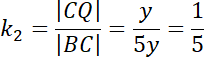
Trójkąty PCQ i ACP są podobne z cechy BKB – stosunek długości odpowiadających sobie boków w obu trójkątach jest taki sam oraz kąt pomiędzy nimi ma taką samą miarę.
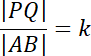
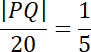
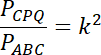
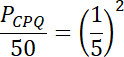
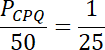
Wykonaj rysunek pomocniczy.
Zauważ, że trójkąty są podobne, gdy spełniona jest jedna z cech: BBB – stosunek długości odpowiadających sobie boków w obu trójkątach jest taki sam, BKB – stosunek długości dwóch odpowiadających sobie boków w obu trójkątach jest taki sam oraz kąt zawarty między nimi w jednym trójkącie jest taki sam jak kąt zawarty pomiędzy nimi w drugim trójkącie, KKK – odpowiadające sobie kąty mają równe miary.
Na tej podstawie wykaż, że trójkąty przedstawione na rysunku spełniają jedną z powyższych cech.
Następnie zauważ, że odpowiadające sobie boki w obu figurach są podobne w wyznaczonej skali
. Zapisz te proporcje z szukaną długościami boku PQ i wyznacz ich wartość.
Zauważ również, że jeśli skala podobieństwa dwóch figur wynosi
, to stosunek ich pól jest równy
. Pod powstałe równanie podstaw znane wartości i z powstałego równania wyznacz wartość pola trójkąta CPQ
Zadanie 1
242Ćwiczenie 1
243Ćwiczenie 2
244Zadanie 1
244Zadanie 4
245Zadanie 9
245Ćwiczenie 2
247Ćwiczenie 3
247Ćwiczenie 7
249Zadanie 1
249Zadanie 8
250Zadanie 9
250Ćwiczenie 1
251Ćwiczenie 2
251Ćwiczenie 4
252Ćwiczenie 5
252Ćwiczenie 7
253Zadanie 1
253Zadanie 5
253Zadanie 7
254Ćwiczenie 1
255Ćwiczenie 2
255Ćwiczenie 3
256Ćwiczenie 4
257Ćwiczenie 5
257Zadanie 1
257Zadanie 3
257Zadanie 5
258Zadanie 12
258Zadanie 13
258Ćwiczenie 2
259Ćwiczenie 3
259Ćwiczenie 5
260Zadanie 2
260Zadanie 3
261Zadanie 4
261Zadanie 5
261Zadanie 6
261Zadanie 7
261Zadanie 9
262Zadanie 10
262Zadanie 11
262Zadanie 12
262Zadanie 13
262Zadanie 1
263Zadanie 2
263Zadanie 4
263Ćwiczenie 1
264Ćwiczenie 3
265Ćwiczenie 5
265Ćwiczenie 6
265Zadanie 1
266Zadanie 3
266Zadanie 5
266Zadanie 13
267Zadanie 14
267Ćwiczenie 1
269Zadanie 1
270Zadanie 5
270Zadanie 1
273Zadanie 3
273Zadanie 4
273Zadanie 1
274Zadanie 2
274Zadanie 3
274Zadanie 4
274Zadanie 6
274