Wykaż, że jeśli wysokość trójkąta zawiera się w jego dwusiecznej, to jest on równoramienny.
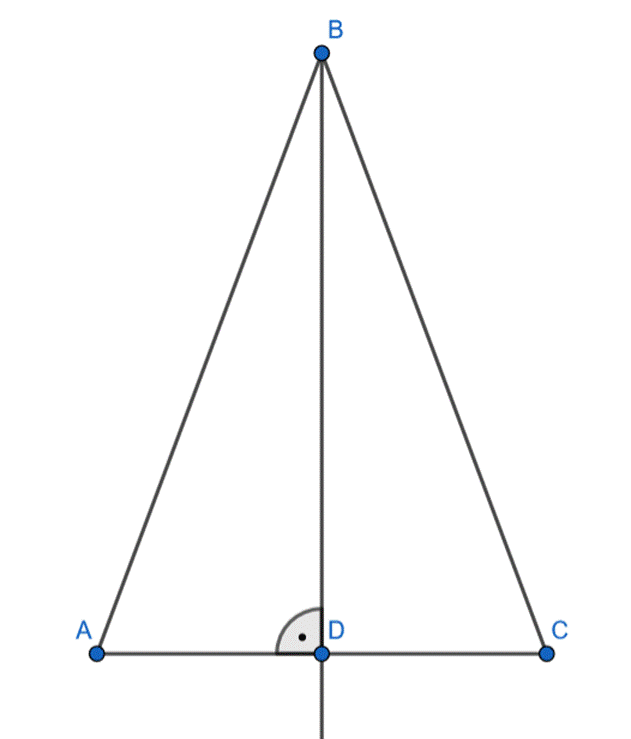
Dwusieczna dzieli kąt na dwa o takiej samej mierze, więc:
![]()
Oznacza to, że trójkąty ABD i CBD są przystające z cechy KBK
![]() .
.
Skoro powyższe trójkąty są przystające, to odpowiadające sobie boki mają takie same długości, więc:
![]()
Czyli trójkąt ABC, którego wysokość zawiera się w dwusiecznej kąta jest równoramienny.
To kończy dowód.


Zadanie 1
242Ćwiczenie 1
243Ćwiczenie 2
244Zadanie 1
244Zadanie 4
245Zadanie 9
245Ćwiczenie 2
247Ćwiczenie 3
247Ćwiczenie 7
249Zadanie 1
249Zadanie 8
250Zadanie 9
250Ćwiczenie 1
251Ćwiczenie 2
251Ćwiczenie 4
252Ćwiczenie 5
252Ćwiczenie 7
253Zadanie 1
253Zadanie 5
253Zadanie 7
254Ćwiczenie 1
255Ćwiczenie 2
255Ćwiczenie 3
256Ćwiczenie 4
257Ćwiczenie 5
257Zadanie 1
257Zadanie 3
257Zadanie 5
258Zadanie 12
258Zadanie 13
258Ćwiczenie 2
259Ćwiczenie 3
259Ćwiczenie 5
260Zadanie 2
260Zadanie 3
261Zadanie 4
261Zadanie 5
261Zadanie 6
261Zadanie 7
261Zadanie 9
262Zadanie 10
262Zadanie 11
262Zadanie 12
262Zadanie 13
262Zadanie 1
263Zadanie 2
263Zadanie 4
263Ćwiczenie 1
264Ćwiczenie 3
265Ćwiczenie 5
265Ćwiczenie 6
265Zadanie 1
266Zadanie 3
266Zadanie 5
266Zadanie 13
267Zadanie 14
267Ćwiczenie 1
269Zadanie 1
270Zadanie 5
270Zadanie 1
273Zadanie 3
273Zadanie 4
273Zadanie 1
274Zadanie 2
274Zadanie 3
274Zadanie 4
274Zadanie 6
274
