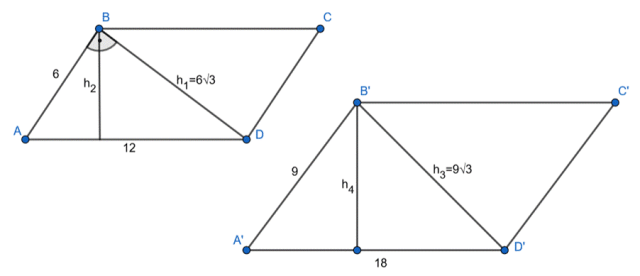
Wyznacz wysokości obu równoległoboków, jeśli dany jest równoległobok ABCD, o bokach 6 cm i 12 cm, jego krótsza przekątna tworzy z jego krótszym bokiem kąt prosty oraz równoległobok A’B’C’D’ jest podobny do równoległoboku ABCD, a jego krótsza przekątna ma długość .

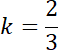
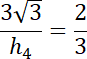
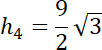
Na podstawie poprzedniego podpunktu znasz długości boków, krótszych przekątnych w obu równoległobokach oraz skalę ich podobieństwa.

Zauważ, że pole równoległoboku jest równe iloczynowi jego wysokości i podstawy na którą odpada pod kątem prostym, więc krótsze przekątne obu z równoległoboków będą jednocześnie ich wysokościami.

Zapisz wzór na pole równoległoboku, podstaw znane długości boków i z powstałego równania wyznacz długość drugiej wysokości równoległoboku ABCD.

Następnie zauważ, że odpowiadające sobie odcinki, w tym wysokości w obu figurach są podobne w wyznaczonej skali . Zapisz te proporcje z szukaną długością wysokości równoległoboku A’B’C’D’ i ją wyznacz.