Wyznacz wartości
![]() i
i
![]() , jeśli
, jeśli
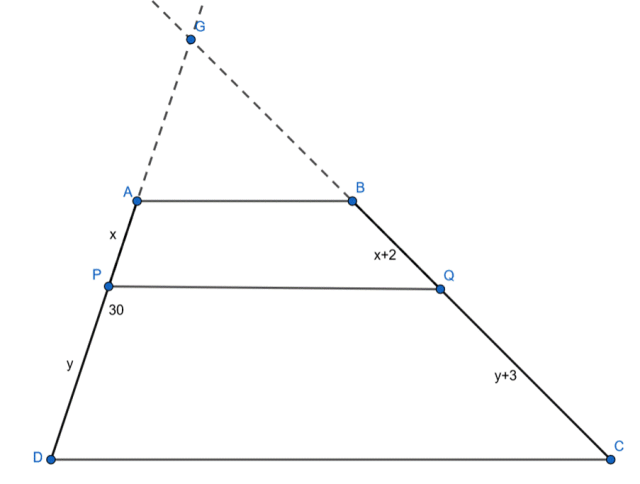
![]() i dany jest trapez ABCD, którego ramię AD ma długość 30 cm, punkt P leży na ramieniu AD, punkt Q na ramieniu BC oraz
i dany jest trapez ABCD, którego ramię AD ma długość 30 cm, punkt P leży na ramieniu AD, punkt Q na ramieniu BC oraz
![]() .
.
Z twierdzenia Talesa:
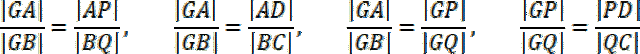
Więc:

Co ostatecznie daje:
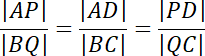
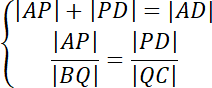
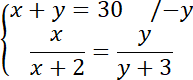
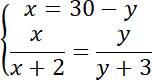
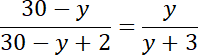
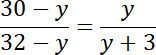
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Wykonaj rysunek pomocniczy.
Skorzystaj z twierdzenia Talesa mówiącego o tym, że jeśli ramiona kąta są przecięte dwoma prostymi równoległymi, to długości odcinków wyznaczonych przez te proste na jednym ramieniu tego kąta są proporcjonalne do długości odpowiednich odcinków wyznaczonych przez te proste na drugim ramieniu i na tej podstawie wypisz proporcje pomiędzy powstałymi odcinkami.
Pod uzyskane proporcje podstaw długości boków znajdujące się na rysunku. Zauważ, że powstanie układ dwóch równań z dwiema niewiadomymi. Wyznacz
![]() z pierwszego i podstaw jego wartość pod drugie. Z uzyskanego równania wyznacz wartość
z pierwszego i podstaw jego wartość pod drugie. Z uzyskanego równania wyznacz wartość
![]() i podstaw ją pod równanie w którym wyznaczony jest
i podstaw ją pod równanie w którym wyznaczony jest
![]() .
.
Na koniec podaj długości odcinków AP, PD, BQ i QC.

Zadanie 1
242Ćwiczenie 1
243Ćwiczenie 2
244Zadanie 1
244Zadanie 4
245Zadanie 9
245Ćwiczenie 2
247Ćwiczenie 3
247Ćwiczenie 7
249Zadanie 1
249Zadanie 8
250Zadanie 9
250Ćwiczenie 1
251Ćwiczenie 2
251Ćwiczenie 4
252Ćwiczenie 5
252Ćwiczenie 7
253Zadanie 1
253Zadanie 5
253Zadanie 7
254Ćwiczenie 1
255Ćwiczenie 2
255Ćwiczenie 3
256Ćwiczenie 4
257Ćwiczenie 5
257Zadanie 1
257Zadanie 3
257Zadanie 5
258Zadanie 12
258Zadanie 13
258Ćwiczenie 2
259Ćwiczenie 3
259Ćwiczenie 5
260Zadanie 2
260Zadanie 3
261Zadanie 4
261Zadanie 5
261Zadanie 6
261Zadanie 7
261Zadanie 9
262Zadanie 10
262Zadanie 11
262Zadanie 12
262Zadanie 13
262Zadanie 1
263Zadanie 2
263Zadanie 4
263Ćwiczenie 1
264Ćwiczenie 3
265Ćwiczenie 5
265Ćwiczenie 6
265Zadanie 1
266Zadanie 3
266Zadanie 5
266Zadanie 13
267Zadanie 14
267Ćwiczenie 1
269Zadanie 1
270Zadanie 5
270Zadanie 1
273Zadanie 3
273Zadanie 4
273Zadanie 1
274Zadanie 2
274Zadanie 3
274Zadanie 4
274Zadanie 6
274
