Oblicz obwód każdego z trójkątów, jeśli suma pól dwóch trójkątów równoramiennych prostokątnych jest równa 180 cm2, a skala ich podobieństwa wynosi 3.
![]() – pole pierwszego trójkąta
– pole pierwszego trójkąta
![]() – pole drugiego trójkąta
– pole drugiego trójkąta
![]()
![]()
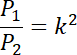
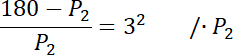
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
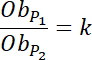

![]()

Na podstawie treści zadania znasz sumę pól powyższych figur. Z powstałego równania wyznacz wartość pola figury P1.
Skorzystaj z tego, że trójkąty P1 i P2 są podobne i na tej podstawie zapisz stosunek ich pól. Zauważ, że jeśli skala podobieństwa dwóch figur wynosi
![]() , to stosunek ich pól jest równy
, to stosunek ich pól jest równy
![]() .
.
Pod powstałe równanie podstaw znane wartości i z powstałego równania wyznacz wartość pola drugiej figury.
Znasz już pole trójkąta P2 i na tej podstawie oblicz pole trójkąta P1.
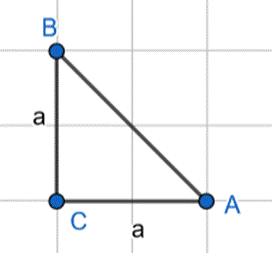
Ze wzoru na pole trójkąta wyznacz długość jego ramienia trójkąta P2. Skorzystaj z twierdzenia Pitagorasa i na tej podstawie oblicz długość przeciwprostokątnej AC tego trójkąta, a następnie oblicz jego obwód.
Skorzystaj z tego, że znasz skalę podobieństwa figur P1 i P2. Więc ich obwody będą podobne w takiej samej skali. Pod powstałe równanie podstaw znane wartości i wyznacz z niego wartości obwodu trójkąta P1.

Zadanie 1
242Ćwiczenie 1
243Ćwiczenie 2
244Zadanie 1
244Zadanie 4
245Zadanie 9
245Ćwiczenie 2
247Ćwiczenie 3
247Ćwiczenie 7
249Zadanie 1
249Zadanie 8
250Zadanie 9
250Ćwiczenie 1
251Ćwiczenie 2
251Ćwiczenie 4
252Ćwiczenie 5
252Ćwiczenie 7
253Zadanie 1
253Zadanie 5
253Zadanie 7
254Ćwiczenie 1
255Ćwiczenie 2
255Ćwiczenie 3
256Ćwiczenie 4
257Ćwiczenie 5
257Zadanie 1
257Zadanie 3
257Zadanie 5
258Zadanie 12
258Zadanie 13
258Ćwiczenie 2
259Ćwiczenie 3
259Ćwiczenie 5
260Zadanie 2
260Zadanie 3
261Zadanie 4
261Zadanie 5
261Zadanie 6
261Zadanie 7
261Zadanie 9
262Zadanie 10
262Zadanie 11
262Zadanie 12
262Zadanie 13
262Zadanie 1
263Zadanie 2
263Zadanie 4
263Ćwiczenie 1
264Ćwiczenie 3
265Ćwiczenie 5
265Ćwiczenie 6
265Zadanie 1
266Zadanie 3
266Zadanie 5
266Zadanie 13
267Zadanie 14
267Ćwiczenie 1
269Zadanie 1
270Zadanie 5
270Zadanie 1
273Zadanie 3
273Zadanie 4
273Zadanie 1
274Zadanie 2
274Zadanie 3
274Zadanie 4
274Zadanie 6
274
