Musisz udowodnić podaną zależność boków trójkąta z polecenia.
Romb AMNP z definicji ma długości wszystkich boków równe. Dla uproszczenia zapisów oznaczmy:
![]()
Pary odcinków |AM| i |PN| oraz |MN| i |AP| są względem siebie równoległe, co oznacza, że:
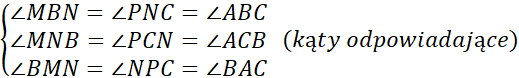
A więc trójkąty ABC, MBN, NPC są do siebie podobne z cechy kąt – kąt – kąt.
Możemy więc zapisać następującą zależność wynikającą z cechy podobnych figur (stały stosunek odpowiadających sobie boków):
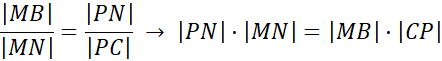
Podstawiając założoną zmienną:
![]()


Zadanie 1.1.
146Zadanie 1.4.
147Zadanie 1.8.
147Zadanie 1.13.
147Zadanie 1.18.
148Zadanie 1.19.
148Zadanie 1.24.
148Zadanie 1.27.
148Zadanie 2.1.
159Zadanie 2.2.
159Zadanie 2.7.
159Zadanie 2.12.
148Zadanie 3.3.
174Zadanie 3.12.
175Zadanie 3.13.
175Zadanie 3.15.
176Zadanie 4.2.
183Zadanie 4.3.
184Zadanie 4.4.
184Zadanie 4.6.
184Zadanie 4.7.
184Zadanie 4.8.
184Zadanie 4.9.
184Zadanie Prosto do matury 5.
186Zadanie 5.2.
192Zadanie 5.3.
192Zadanie 5.6.
193Zadanie 5.7.
193Zadanie 5.9.
193Zadanie 6.2.
208Zadanie 6.3.
209Zadanie 6.4.
209Zadanie 6.5.
209Zadanie 6.10.
210Zadanie 30.
217Zadanie 39.
218
