Skonstruuj płaszczyznę, z której odcinek AB jest widoczny pod kątem 30°.
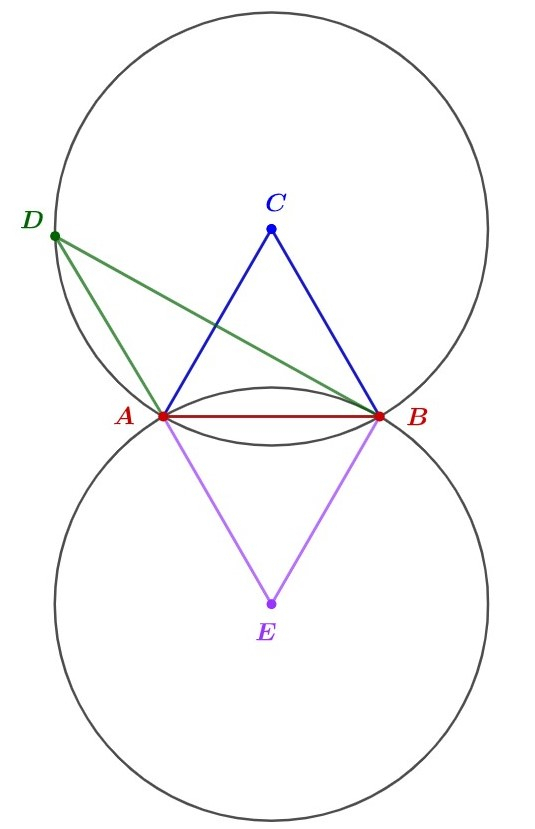

1. Narysuj dowolny odcinek AB.
2. Wykreśl łuki, używając cyrkla o rozwartości długości odcinka AB, z punktów końcowych odcinka tak, aby miały one punkt wspólny.
3. Połącz ze sobą wszystkie trzy punkty, będące wierzchołkami trójkąta równobocznego.
4. Wykreśl za pomocą cyrkla okrąg o promieniu równym długości odcinka AB z punktu przecięcia łuków.
5. Na powstałym okręgu wyznacz dowolny punkt, kąt wyznaczony przez ten punkt jest dwa razy mniejszy od kąta w trójkącie równobocznym, czyli 30° (własności kątów wpisanych i środkowych opartych na tym samym łuku AB)
6. Skonstruuj analogicznie przypadek symetryczny względem odcinka AB.
7. Punkty płaszczyzny spełniające warunki zadania znajdują się na większym łuku AB w powstałych okręgach.

Zadanie 1.1.
146Zadanie 1.4.
147Zadanie 1.8.
147Zadanie 1.13.
147Zadanie 1.18.
148Zadanie 1.19.
148Zadanie 1.24.
148Zadanie 1.27.
148Zadanie 2.1.
159Zadanie 2.2.
159Zadanie 2.7.
159Zadanie 2.12.
148Zadanie 3.3.
174Zadanie 3.12.
175Zadanie 3.13.
175Zadanie 3.15.
176Zadanie 4.2.
183Zadanie 4.3.
184Zadanie 4.4.
184Zadanie 4.6.
184Zadanie 4.7.
184Zadanie 4.8.
184Zadanie 4.9.
184Zadanie Prosto do matury 5.
186Zadanie 5.2.
192Zadanie 5.3.
192Zadanie 5.6.
193Zadanie 5.7.
193Zadanie 5.9.
193Zadanie 6.2.
208Zadanie 6.3.
209Zadanie 6.4.
209Zadanie 6.5.
209Zadanie 6.10.
210Zadanie 30.
217Zadanie 39.
218
