Musisz obliczyć pole opisanego trójkąta wykorzystując zależności podobnych trójkątów.
Pole opisanego trójkąta wynosi 432 cm2.

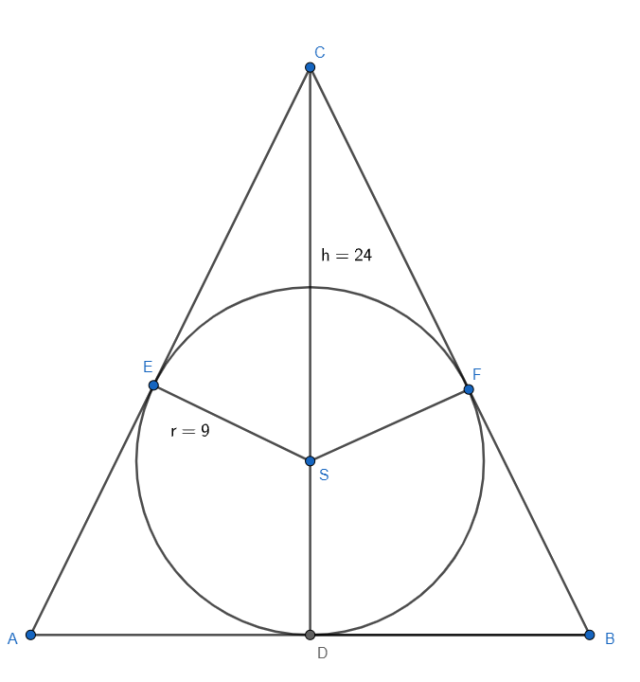
Przyjmując oznaczenia zgodnie z rysunkiem powyżej, możemy zauważyć, że:
![]()
![]()
Z twierdzenia Pitagorasa możemy obliczyć pozostałą długość przyprostokątnej trójkąta CES:
![]()
Możemy zauważyć, że:
![]()
Więc trójkąty ACD oraz CES są do siebie podobne z cechy kąt – kąt – kąt. Skalę podobieństwa k możemy obliczyć na podstawie porównania dłuższych przyprostokątnych:
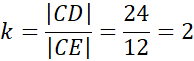
Możemy więc obliczyć:
![]()
Pole trójkąta wynosi więc:
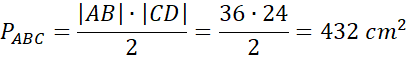

Zadanie 1.1.
146Zadanie 1.4.
147Zadanie 1.8.
147Zadanie 1.13.
147Zadanie 1.18.
148Zadanie 1.19.
148Zadanie 1.24.
148Zadanie 1.27.
148Zadanie 2.1.
159Zadanie 2.2.
159Zadanie 2.7.
159Zadanie 2.12.
148Zadanie 3.3.
174Zadanie 3.12.
175Zadanie 3.13.
175Zadanie 3.15.
176Zadanie 4.2.
183Zadanie 4.3.
184Zadanie 4.4.
184Zadanie 4.6.
184Zadanie 4.7.
184Zadanie 4.8.
184Zadanie 4.9.
184Zadanie Prosto do matury 5.
186Zadanie 5.2.
192Zadanie 5.3.
192Zadanie 5.6.
193Zadanie 5.7.
193Zadanie 5.9.
193Zadanie 6.2.
208Zadanie 6.3.
209Zadanie 6.4.
209Zadanie 6.5.
209Zadanie 6.10.
210Zadanie 30.
217Zadanie 39.
218
