Musisz wykazać, że odcinki PM i PN są równej długości, a co za tym idzie punkt P jest środkiem boku MN.
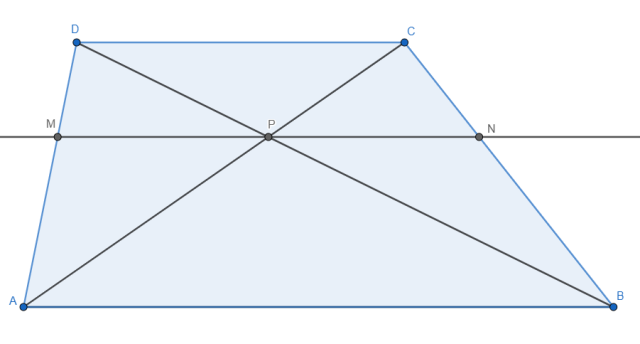
Trójkąty ACD i APM są do siebie podobne z cechy kąt – kąt – kąt, więc możemy zapisać:
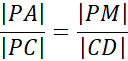
Trójkąty BCD i BPN są do siebie podobne z cechy kąt – kąt – kąt, więc możemy zapisać:
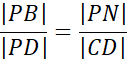
Trójkąty ABP i CDP są do siebie podobne z cechy kąt – kąt – kąt, więc możemy zapisać:
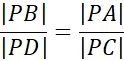
Podstawiając wcześniej wyprowadzone zależności:
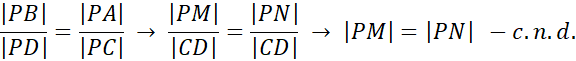


Zadanie 1.1.
146Zadanie 1.4.
147Zadanie 1.8.
147Zadanie 1.13.
147Zadanie 1.18.
148Zadanie 1.19.
148Zadanie 1.24.
148Zadanie 1.27.
148Zadanie 2.1.
159Zadanie 2.2.
159Zadanie 2.7.
159Zadanie 2.12.
148Zadanie 3.3.
174Zadanie 3.12.
175Zadanie 3.13.
175Zadanie 3.15.
176Zadanie 4.2.
183Zadanie 4.3.
184Zadanie 4.4.
184Zadanie 4.6.
184Zadanie 4.7.
184Zadanie 4.8.
184Zadanie 4.9.
184Zadanie Prosto do matury 5.
186Zadanie 5.2.
192Zadanie 5.3.
192Zadanie 5.6.
193Zadanie 5.7.
193Zadanie 5.9.
193Zadanie 6.2.
208Zadanie 6.3.
209Zadanie 6.4.
209Zadanie 6.5.
209Zadanie 6.10.
210Zadanie 30.
217Zadanie 39.
218
