Musisz obliczyć długość zadanego odcinka za pomocą podobieństwa trójkątów.
Długość wspólnego boku tych figur wynosi:
![]()

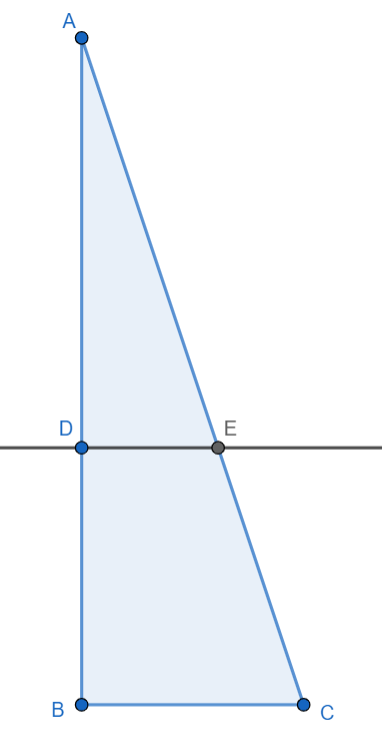
Przyjmując oznaczenia zgodnie z rysunkiem powyżej, możemy zapisać, że:
Trójkąt ADE jest podobny do trójkąta ABC z cechy kąt – kąt – kąt w skali opisanej zmienną k:
![]()
![]()
Wiemy, że pola figur ADE oraz BCED są sobie równe, oraz ich suma równa się polu trójkąta ABC, możemy więc zapisać:
![]()
Zapiszmy wzór na pole trójkąta ADE:
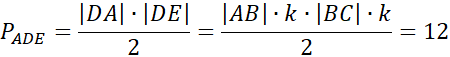
Podstawiając znane wartości:
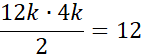
![]()
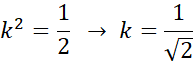
Obliczając zadaną wartość:
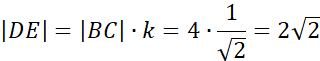

Zadanie 1.1.
146Zadanie 1.4.
147Zadanie 1.8.
147Zadanie 1.13.
147Zadanie 1.18.
148Zadanie 1.19.
148Zadanie 1.24.
148Zadanie 1.27.
148Zadanie 2.1.
159Zadanie 2.2.
159Zadanie 2.7.
159Zadanie 2.12.
148Zadanie 3.3.
174Zadanie 3.12.
175Zadanie 3.13.
175Zadanie 3.15.
176Zadanie 4.2.
183Zadanie 4.3.
184Zadanie 4.4.
184Zadanie 4.6.
184Zadanie 4.7.
184Zadanie 4.8.
184Zadanie 4.9.
184Zadanie Prosto do matury 5.
186Zadanie 5.2.
192Zadanie 5.3.
192Zadanie 5.6.
193Zadanie 5.7.
193Zadanie 5.9.
193Zadanie 6.2.
208Zadanie 6.3.
209Zadanie 6.4.
209Zadanie 6.5.
209Zadanie 6.10.
210Zadanie 30.
217Zadanie 39.
218
