Wyznacz konstrukcyjnie trójkąt, którego środkami boków są trzy dowolne punkty nie współliniowe.
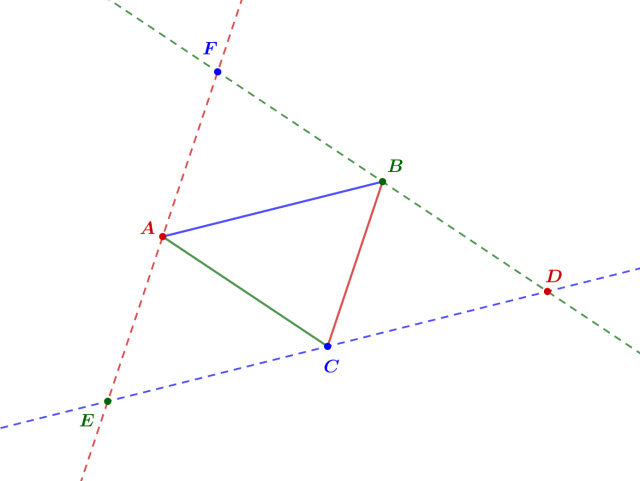

1. Zaznacz trzy dowolne punkty nie współliniowe (A, B, C).
2. Połącz te punkty odcinkami tworząc trójkąt ABC.
3. Poprowadź trzy proste – każdą równoległą do boków trójkąta ABC i przechodząca przez trzeci jego wierzchołek.
4. Punkty przecięcia każdych dwóch tych prostych wyznaczają wierzchołki (D, E, F)
5. Na mocy twierdzenia o odcinkach łączących środki boków trójkąta, punkty A, B i C są środkami boków trójkąta DEF.

Zadanie 1.1.
146Zadanie 1.4.
147Zadanie 1.8.
147Zadanie 1.13.
147Zadanie 1.18.
148Zadanie 1.19.
148Zadanie 1.24.
148Zadanie 1.27.
148Zadanie 2.1.
159Zadanie 2.2.
159Zadanie 2.7.
159Zadanie 2.12.
148Zadanie 3.3.
174Zadanie 3.12.
175Zadanie 3.13.
175Zadanie 3.15.
176Zadanie 4.2.
183Zadanie 4.3.
184Zadanie 4.4.
184Zadanie 4.6.
184Zadanie 4.7.
184Zadanie 4.8.
184Zadanie 4.9.
184Zadanie Prosto do matury 5.
186Zadanie 5.2.
192Zadanie 5.3.
192Zadanie 5.6.
193Zadanie 5.7.
193Zadanie 5.9.
193Zadanie 6.2.
208Zadanie 6.3.
209Zadanie 6.4.
209Zadanie 6.5.
209Zadanie 6.10.
210Zadanie 30.
217Zadanie 39.
218
