


1. Aby rozwiązać tego typu zadania, musimy skorzystać z równania Clapeyrona. Równanie to obrazuje zależności między ilością gazu (w molach), objętością a warunkami (ciśnieniem i temperaturą):
p ∙ V = n ∙ R ∙ T, gdzie:
n — liczba moli gazu
P — ciśnienie [hPa]
V — objętość [dm3]
R — stała gazowa
T — temperatura [K]
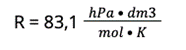
2. Z równania wynika, że musimy znać liczbę moli chloru. Chlor występuje w cząsteczkach dwuatomowych, więc masa cząsteczki to 2 ∙ masa atomu chloru = 2 ∙ 35,5 g/mol = 71 g/mol = 0,071 kg/mol
Skoro 1 mol chloru to 0,071 kg, możemy obliczyć ile moli jest równe 5 kg chloru:
0,071 kg — 1 mol
5 kg — x
x = 5 ∙ 1 : 0,071 = 70,42 [mol] — wartość n
3. Znane wartości należy podstawić do równania Clapeyrona. Warunki normalne od standardowych różnią się temperaturą. W obu przypadkach ciśnienie wynosi 1013 hPa, a stała gazowa R pozostaje bez zmian.
Warunki normalne to temperatura 293 K, a standardowe – 298 K.
4. Dane należy podstawić do wzoru i rozwiązać równania.
∙ Warunki standardowe:
pV = nRT
1013 ∙ V = 70,42 ∙ 83,1 ∙ 298
1013 ∙ V = 1743866,8 / : 1013
V = 1721,5 [dm3]
∙ Warunki normalne:
pV = nRT
1013 ∙ V = 70,42 ∙ 83,1 ∙ 273
1013 ∙ V = 1597569,25 / : 1013
V = 1577,1 [dm3]