W tym zadaniu musisz udowodnić, że w czworokąt można wpisać okrąg, przecinający wszystkie boki czworokąta i wycinający na nich równe odcinki.
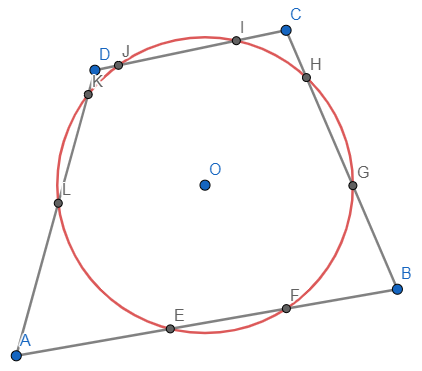
Z twierdzenia o siecznych mamy, iż ![]()
![]()
Zachodzi to dla każdego wierzchołka, zatem:
![]()
Dowodzi to możliwości wpisania okręgu w czworokąt ABCD.

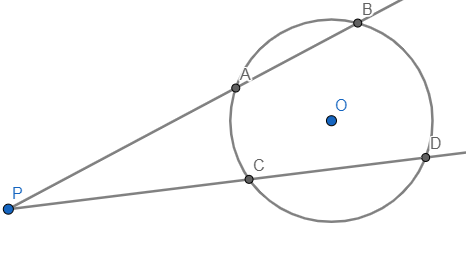
Twierdzenie o siecznych mówi, iż sieczne danego okręgu, wychodzące z jednego punktu P i przecinające okrąg w punktach A, B, C i D, przechodzą przez ten okrąg tak, że:
![]()

Ćwiczenie 5.
12Zadanie 1.
15Zadanie 2.
15Zadanie 3.
15Zadanie 4.
15Zadanie 5.
15Zadanie 6.
15Zadanie 14.
16Ćwiczenie 1.
19Zadanie 1.
24Zadanie 2.
24Ćwiczenie 1.
30Ćwiczenie 2.
31Zadanie 1.
32Zadanie 2.
32Zadanie 1.
39Zadanie 2.
39Zadanie 3.
39Zadanie 4.
39Ćwiczenie 1.
65Ćwiczenie 1.
71Ćwiczenie 2.
71Zadanie 1.
74Zadanie 2.
74Ćwiczenie 1.
80Zadanie 1.
84Zadanie 1.
93Ćwiczenie 1.
101Zadanie 1.
105Zadanie 2.
105
