W tym zadaniu musisz obliczyć, ile razy pole trójkąta ABC jest większe od EFG.
![]()
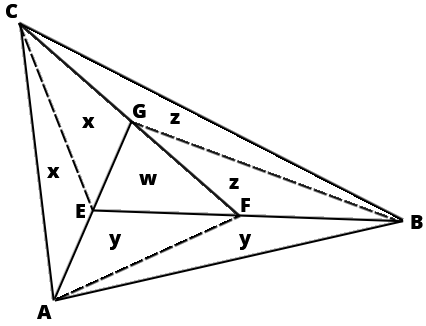
Po poprowadzeniu linii pomocniczych mamy:
![]()
![]()
![]()
![]()
Przyjrzyjmy się trójkątowi ABG. Odcinek AE jest równy odcinkowi EG, zaś wysokości są równe. Stąd:
![]()
Analogicznie dla trójkątów AFC i BCE:
![]()
![]()
Otrzymujemy układ 3 równań:
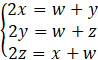
Wyznaczamy z pierwszego x:
![]()
Wyznaczamy z drugiego y:
![]()
Podstawiamy y do wyrażenia na x:
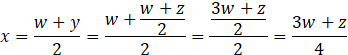
Wstawiamy tak wyrażonego x do trzeciego równania:
![]()
![]()
![]()
Zamieniając w na z w trzecim równaniu:
![]()
W pierwszym równaniu podmieniamy x i w na z:
![]()
Stąd rozwiązanie:
![]()
Jeśli wszystkie pola są sobie równe, to ![]()

Poprowadź linie pomocnicze i zwróć uwagę na 2 fakty. Stosunek podziału pól np. trójkątów BGE i BEA odcinkiem ![]()

Ćwiczenie 5.
12Zadanie 1.
15Zadanie 2.
15Zadanie 3.
15Zadanie 4.
15Zadanie 5.
15Zadanie 6.
15Zadanie 14.
16Ćwiczenie 1.
19Zadanie 1.
24Zadanie 2.
24Ćwiczenie 1.
30Ćwiczenie 2.
31Zadanie 1.
32Zadanie 2.
32Zadanie 1.
39Zadanie 2.
39Zadanie 3.
39Zadanie 4.
39Ćwiczenie 1.
65Ćwiczenie 1.
71Ćwiczenie 2.
71Zadanie 1.
74Zadanie 2.
74Ćwiczenie 1.
80Zadanie 1.
84Zadanie 1.
93Ćwiczenie 1.
101Zadanie 1.
105Zadanie 2.
105
