W tym zadaniu musisz udowodnić, iż punkty B, C, D i E leżą na okręgu, biorąc pod uwagę, że dwa okręgi przecinają się w punktach A i B. Ponadto poprowadzono prostą przechodzącą przez punkt A, która przecięła okręgi w punktach C i D, oraz że przez punkty C i D przeprowadzono styczne do tych okręgów, które przecięły się w punkcie E.
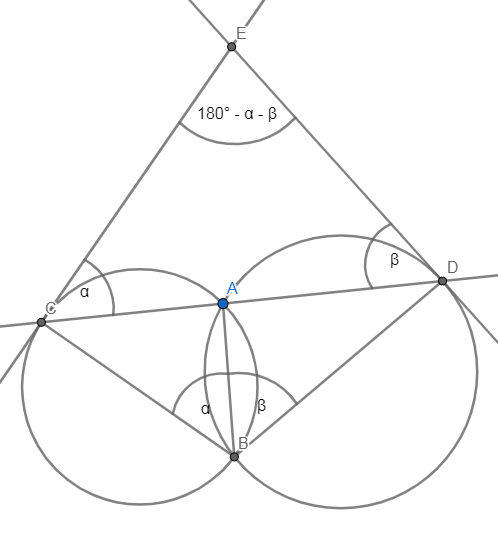
Prowadzimy odcinek AB. Między styczną EC a cięciwą CA jest kąt ![]()
![]()
![]()
![]()
Czworokąt CBDE można wpisać w okrąg.

Rozpisz kąty ![]()
![]()
![]()

Ćwiczenie 5.
12Zadanie 1.
15Zadanie 2.
15Zadanie 3.
15Zadanie 4.
15Zadanie 5.
15Zadanie 6.
15Zadanie 14.
16Ćwiczenie 1.
19Zadanie 1.
24Zadanie 2.
24Ćwiczenie 1.
30Ćwiczenie 2.
31Zadanie 1.
32Zadanie 2.
32Zadanie 1.
39Zadanie 2.
39Zadanie 3.
39Zadanie 4.
39Ćwiczenie 1.
65Ćwiczenie 1.
71Ćwiczenie 2.
71Zadanie 1.
74Zadanie 2.
74Ćwiczenie 1.
80Zadanie 1.
84Zadanie 1.
93Ćwiczenie 1.
101Zadanie 1.
105Zadanie 2.
105
