W tym zadaniu musisz udowodnić, iż średnica okręgu jest równa średniej geometrycznej długości podstaw trapezu..
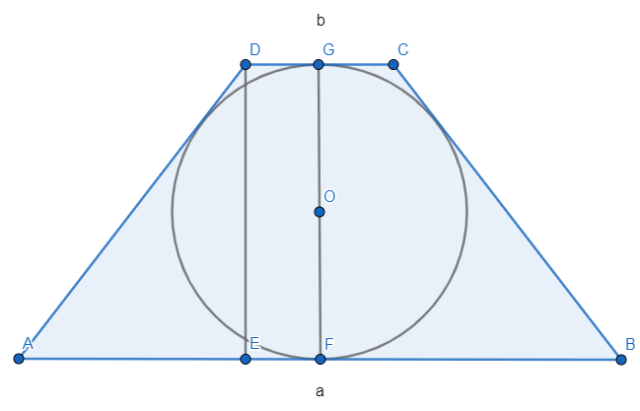
Z faktu, iż okrąg jest wpisany w trapez:
![]()
Nierównoległe boki mają równe długości, stąd:
![]()
Odcinek AE:
![]()
Korzystamy następnie z twierdzenia Pitagorasa:
![]()
![]()
![]()
Promień to zatem średnia geometryczna długości podstaw.

Skorzystaj z faktu, iż trapez jest opisany na okręgu, z twierdzenia Pitagorasa oraz z definicji średniej geometrycznej. Mianowicie, średnia geometryczna n liczb dodatnich to wyrażenie:
![]()
Masz dwie liczby (a i b), zatem pierwiastek jest drugiego stopnia.

Ćwiczenie 5.
12Zadanie 1.
15Zadanie 2.
15Zadanie 3.
15Zadanie 4.
15Zadanie 5.
15Zadanie 6.
15Zadanie 14.
16Ćwiczenie 1.
19Zadanie 1.
24Zadanie 2.
24Ćwiczenie 1.
30Ćwiczenie 2.
31Zadanie 1.
32Zadanie 2.
32Zadanie 1.
39Zadanie 2.
39Zadanie 3.
39Zadanie 4.
39Ćwiczenie 1.
65Ćwiczenie 1.
71Ćwiczenie 2.
71Zadanie 1.
74Zadanie 2.
74Ćwiczenie 1.
80Zadanie 1.
84Zadanie 1.
93Ćwiczenie 1.
101Zadanie 1.
105Zadanie 2.
105
