W tym zadaniu musisz obliczyć pole i obwód zakreskowanej figury. Pamiętaj, iż wierzchołki sześciokąta foremnego ABCDEF o boku długości 6 są środkami kół o promieniach długości 3. Na rysunku zaś zaznaczono wycinki tychże kół.
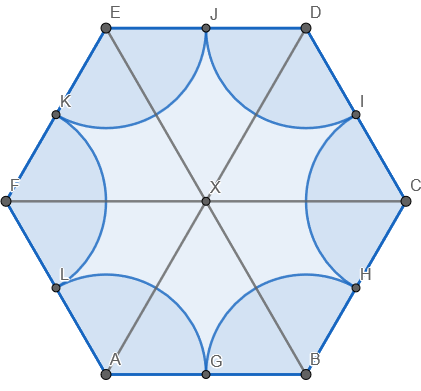
Oznaczając pole okręgu o promieniu 3 jako S z indeksem o:
![]()
Pole powierzchni sześciokąta:
![]()
![]()
![]()

Prowadząc przekątne, zauważ, iż figurę można podzielić na 6 trójkątów równobocznych, gdyż dwa z boków są równe, zaś kąty wewnętrzne wynoszą ![]()
![]()
![]()
![]()
![]()
Pole powierzchni sześciokąta jest równe sumie pól trójkątów równobocznych:
![]()
Poszukiwane pole wynosi:
![]()
Obwód jest równy dwukrotności obwodu koła o promieniu 3:
![]()

Ćwiczenie 5.
12Zadanie 1.
15Zadanie 2.
15Zadanie 3.
15Zadanie 4.
15Zadanie 5.
15Zadanie 6.
15Zadanie 14.
16Ćwiczenie 1.
19Zadanie 1.
24Zadanie 2.
24Ćwiczenie 1.
30Ćwiczenie 2.
31Zadanie 1.
32Zadanie 2.
32Zadanie 1.
39Zadanie 2.
39Zadanie 3.
39Zadanie 4.
39Ćwiczenie 1.
65Ćwiczenie 1.
71Ćwiczenie 2.
71Zadanie 1.
74Zadanie 2.
74Ćwiczenie 1.
80Zadanie 1.
84Zadanie 1.
93Ćwiczenie 1.
101Zadanie 1.
105Zadanie 2.
105
