W tym zadaniu musisz udowodnić równość pól czworokątów.
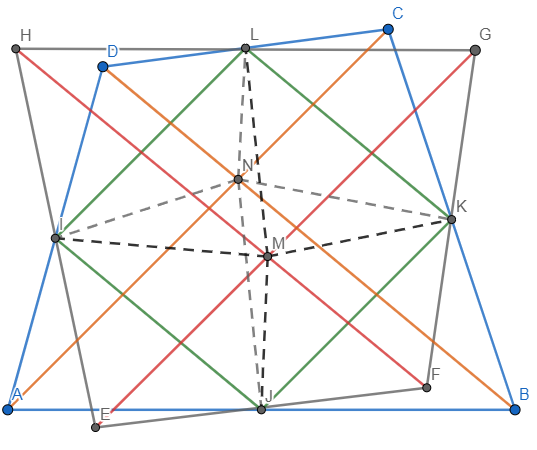
Czworokąty ABCD i EFGH mają wspólne środki boków. Łączymy te środki tworząc czworokąt IJKL (zielony). Czerwone odcinki to przekątne EFGH, zaś pomarańczowe to przekątne ABCD. Punkty przecięcia przekątnych (M i N) łączymy ze środkami boków (czyli IJKL). Odcinek IL jest równy połowie AC i połowie EG (twierdzenie o środkowej trójkąta). Analogicznie pozostałe boki IJKL. Przyglądając się trójkątowi INL widzimy, iż jego pole jest 4 razy mniejsze od pola trójkąta ACD (wysokość INL jest połową wysokości ACD, a podstawa IL jest równa połowie podstawy AC). Tak samo dla czworokąta EFGH pole trójkąta IML jest ![]()
![]()
![]()
Pole IJKL można zapisać na dwa sposoby:
![]()
![]()
Implikuje to równość:
![]()

Dowód można uprościć. Wystarczy zauważyć, iż skoro czworokąt IJKL jest rozpięty zarówno na czworokącie ABCD, jaki i EFGH, to jego pole jest równe połowie zarówno czworokąta ABCD, jak i EFGH. Zatem wyjściowe czworokąty mają równe pola.

Ćwiczenie 5.
12Zadanie 1.
15Zadanie 2.
15Zadanie 3.
15Zadanie 4.
15Zadanie 5.
15Zadanie 6.
15Zadanie 14.
16Ćwiczenie 1.
19Zadanie 1.
24Zadanie 2.
24Ćwiczenie 1.
30Ćwiczenie 2.
31Zadanie 1.
32Zadanie 2.
32Zadanie 1.
39Zadanie 2.
39Zadanie 3.
39Zadanie 4.
39Ćwiczenie 1.
65Ćwiczenie 1.
71Ćwiczenie 2.
71Zadanie 1.
74Zadanie 2.
74Ćwiczenie 1.
80Zadanie 1.
84Zadanie 1.
93Ćwiczenie 1.
101Zadanie 1.
105Zadanie 2.
105
