W tym zadaniu musisz udowodnić, że pola obu równoległoboków są równe. Punkt E leży na boku CD, a punkt A leży na boku FG równoległoboków ABCD i BEFG.
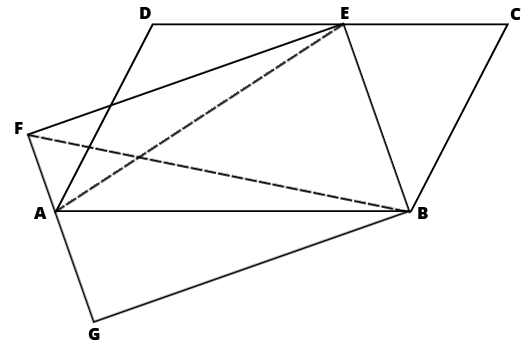
Trójkąt BFG stanowi połowę pola równoległoboku BEFG. Ma on tę samą podstawę i wysokość, co trójkąt ABE, zatem i to samo pole. Implikuje to, iż suma pól trójkątów AEF i AGB również stanowi połowę pola BEFG. Pole trójkąta ABE jest równe połowie pola równoległoboku ABCD (dokładnie z tej samej obserwacji, co dla BEFG), zatem suma pól trójkątów AED i BCE również składa się na połowę pola ABCD. Skoro zachodzą równości ![]()

Trójkąty o równych podstawach i wysokościach mają równe pola.

Ćwiczenie 5.
12Zadanie 1.
15Zadanie 2.
15Zadanie 3.
15Zadanie 4.
15Zadanie 5.
15Zadanie 6.
15Zadanie 14.
16Ćwiczenie 1.
19Zadanie 1.
24Zadanie 2.
24Ćwiczenie 1.
30Ćwiczenie 2.
31Zadanie 1.
32Zadanie 2.
32Zadanie 1.
39Zadanie 2.
39Zadanie 3.
39Zadanie 4.
39Ćwiczenie 1.
65Ćwiczenie 1.
71Ćwiczenie 2.
71Zadanie 1.
74Zadanie 2.
74Ćwiczenie 1.
80Zadanie 1.
84Zadanie 1.
93Ćwiczenie 1.
101Zadanie 1.
105Zadanie 2.
105
