W tym zadaniu musisz udowodnić równość pola czworokąta KMLN i sumy pól trójkątów AKD i BCL. Punkty M i N leżą odpowiednio na bokach AB i CD trapezu ABCD. Odcinki AN i DM przecinają się w punkcie K, zaś odcinki BN i CM przecinają się w punkcie L.
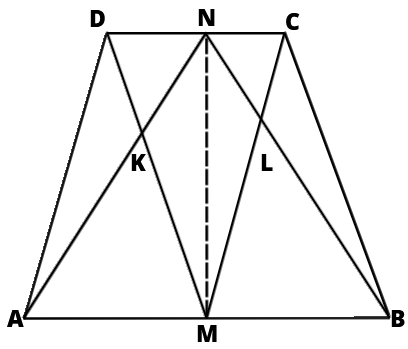
Rozważmy trapezy AMND i MBCN. W trapezie AMND trójkąty AMN i AMD mają te same długości podstawy i wysokości, zatem i równe pola. Skoro tak, to i pola AKD i MNK są równe (gdyż to pola odpowiednio AMD i AMN po odjęciu od nich części AMK). Mamy zatem ![]()
![]()
Pole powierzchni czworokąta KMLN wynosi zatem:
![]()

Trójkąty o równych podstawach i wysokościach mają równe pola.

Ćwiczenie 5.
12Zadanie 1.
15Zadanie 2.
15Zadanie 3.
15Zadanie 4.
15Zadanie 5.
15Zadanie 6.
15Zadanie 14.
16Ćwiczenie 1.
19Zadanie 1.
24Zadanie 2.
24Ćwiczenie 1.
30Ćwiczenie 2.
31Zadanie 1.
32Zadanie 2.
32Zadanie 1.
39Zadanie 2.
39Zadanie 3.
39Zadanie 4.
39Ćwiczenie 1.
65Ćwiczenie 1.
71Ćwiczenie 2.
71Zadanie 1.
74Zadanie 2.
74Ćwiczenie 1.
80Zadanie 1.
84Zadanie 1.
93Ćwiczenie 1.
101Zadanie 1.
105Zadanie 2.
105
