W tym zadaniu musisz udowodnić, iż trójkąt DMC jest równoramienny. Weź pod uwagę, iż przekątne trapezu ABCD przecinają się w punkcie O, zaś okręgi opisane na trójkątach AOD i BOC przecinają się na podstawie AB tego trapezu.
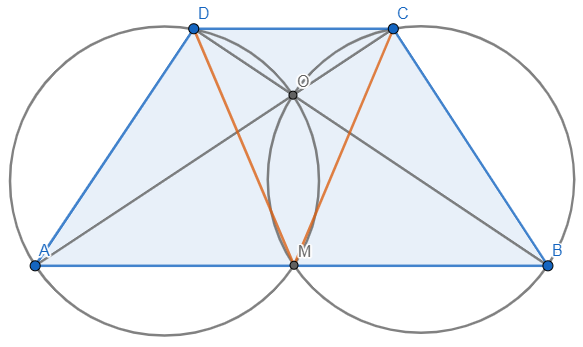
Zauważmy, iż skoro AB jest równoległe do CD, to kąty CDB i OBM są naprzemianległe (są równe, gdyż znajdują się po różnych stronach prostej przecinającej 2 proste równoległe). Analogicznie DCA i OAM są naprzemianległe. Jako, iż OBM oparty jest na tym samym łuku co OCM, to są to te same kąty. Analogicznie ![]()
![]()

Skorzystaj z równości kątów naprzemianległych i opartych na tym samym łuku.

Ćwiczenie 5.
12Zadanie 1.
15Zadanie 2.
15Zadanie 3.
15Zadanie 4.
15Zadanie 5.
15Zadanie 6.
15Zadanie 14.
16Ćwiczenie 1.
19Zadanie 1.
24Zadanie 2.
24Ćwiczenie 1.
30Ćwiczenie 2.
31Zadanie 1.
32Zadanie 2.
32Zadanie 1.
39Zadanie 2.
39Zadanie 3.
39Zadanie 4.
39Ćwiczenie 1.
65Ćwiczenie 1.
71Ćwiczenie 2.
71Zadanie 1.
74Zadanie 2.
74Ćwiczenie 1.
80Zadanie 1.
84Zadanie 1.
93Ćwiczenie 1.
101Zadanie 1.
105Zadanie 2.
105
