Dane:
R = 36 cm = 0,36 m
r = 4,2 cm = 0,042 m
I = 0,38 kg ⋅ m2
F = 5 N
t = 10 s
Moment siły to iloczyn siły, ramienia siły i sinusa kąta pomiędzy nimi:
![]()
![]()
Koło roweru wykonuje ruch obrotowy jednostajnie przyspieszony, z drugiej zasady dynamiki dla ruchu obrotowego:
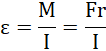
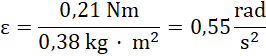
![]()
![]()
![]()
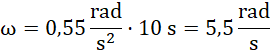
Wektor prędkości kątowej jest prostopadły do koła roweru i przechodzi przez jego środek, jeżeli przyjmiemy, że koło kręci się w zgodnie z ruchem wskazówek zegara, to wektor jest zwrócony przed kartkę.
Odpowiedź: Moment sił działający na zębatkę ma wartość 0,21 Nm, przyspieszenie kątowe wyniosło ![]()
![]()

Pamiętaj, moment siły otrzymasz, mnożąc wartość siły działającej na koło, ramię siły (odległość środka koła od miejsca przyłożenia siły) oraz sinusa pomiędzy tymi wektorami (mamy tutaj kąt prosty, więc sinus jest równy 1). Na koło działa niezrównoważona siła wprawiająca go w ruch obrotowy jednostajnie przyspieszony, z 2. zasady dynamiki dla ruchu obrotowego, przyspieszenie to iloraz momentu siły i momentu bezwładności – wykorzystując poprzednie obliczenia, podaj wartość przyspieszenia. Na koniec przypomnij sobie wzór opisujący prędkość kątową w ruchu jednostajnie zmiennym, gdzie prędkość początkowa wynosi zero – jest to iloczyn czasu trwania ruchu i przyspieszenia kątowego. Wektor prędkości kątowej ma kierunek prostopadły do koła, jego zwrot wyznaczysz, stosując regułę prawej ręki.