Oblicz czas toczenia się bez poślizgu kręgu studziennego o masie 530 kg, którego wymiary to: dw = 1500 mm– średnica wewnętrzna kręgu, dz = 1800 mm – średnica zewnętrzna kręgu, wiedząc, że stok ma długość 80 m, a jego nachylenie wynosi 30°. Przyjmij, że 
Dane:
m = 530 kg
l = 80 m
dw = 1500 mm = 1,5 m
dz = 1800 mm = 1,8 m
α = 30°
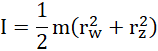
dla ułatwienia przekształceń, niech:
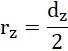
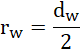
Na krąg działa siła grawitacji, siła tarcia oraz siła reakcji podłoża.
Rozłóżmy siłę grawitacji na składowe:
krąg wykonuje ruch obrotowy jednostajnie przyspieszony, z 2 zasady dynamiki w ruchu obrotowym dla bryły sztywnej:
moment bezwładności kręgu: 
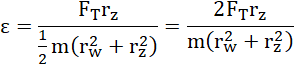
ponadto:
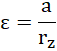
otrzymujemy układ równań:
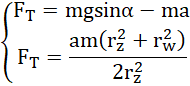
co po przekształceniach daje:
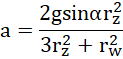
wykorzystując wzór:
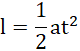
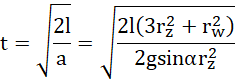
wstawiając w miejsce promieni, średnice:
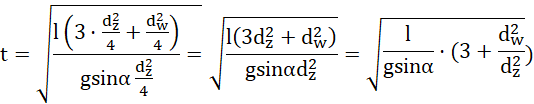
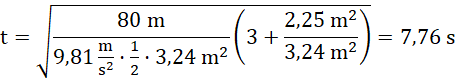
Odpowiedź: Krąg staczał się ze wzniesienia przez 7,76 s.
Na początek zastanów się, jakie siły działają na krąg – jest to siła ciężkości (rozpisz ją na składowe), siła reakcji podłoża oraz siła tarcia. Siła reakcji podłoża równoważy się ze składową siły ciężkości wzdłuż osi y (prostopadłej do zbocza), a suma pozostałych sił, z drugiej zasady dynamiki dla ruchu postępowego, to iloczyn masy i przyspieszenia liniowego kręgu. Ciało wykonuje też ruch obrotowy jednostajnie zmienny (gdyż siła na niego działająca nie jest równoważona), więc przyspieszenie kątowe jest równe ilorazowi wypadkowej momentu sił (tutaj jest to siła tarcia) oraz momentu bezwładności. Z zebranych równości wyznacz siłę tarcia, a po przyrównaniu ich do siebie – przyspieszenie liniowe (przyspieszenie kątowe zapisz jako iloraz przyspieszenia liniowego i promienia zewnętrznego). Gdy znasz już przyspieszenie kręgu, przekształć wzór na drogę w ruchu jednostajnie zmiennym bez prędkości początkowej – wstaw tam przyspieszenie liniowe i wyznacz wartość czasu. Zwróć uwagę, we wzorach wykorzystujemy promienie kręgu, jeżeli dla ułatwienia przekształceń stosujesz je zamiast podanych w treści średnic (jak w rozwiązaniu), nie zapomnij powrócić do nich na końcu zadania.