Wykonaj konieczne obliczenia i podaj warunek dla współczynnika tarcia statycznego, aby ruch kręgu odbywał się bez poślizgu, wiedząc, że krąg o masie 530 kg, którego wymiary to: dw = 1500 mm– średnica wewnętrzna kręgu, dz = 1800 mm – średnica zewnętrzna kręgu toczy się po stoku długości 80 m, którego nachylenie wynosi 30°. Przyjmij, że 
Dane:
m = 530 kg
l = 80 m
dw = 1500 mm = 1,5 m
dz= 1800 mm = 1,8 m
α = 30°
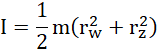
dla ułatwienia przekształceń, niech:
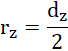
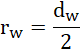
Na krąg działa siła grawitacji, siła tarcia oraz siła reakcji podłoża.
Rozłóżmy siłę grawitacji na składowe:
Aby krąg staczał się bez poślizgu, siła tarcia statycznego musi być większa lub równa od składowej Fgx siły ciężkości
Zbadajmy przypadek graniczny, czyli taki, gdzie współczynnik tarcia statycznego jest możliwie najmniejszy, a ruch odbywa się bez poślizgu
Przekształcając pierwszą równość:
Krąg wykonuje ruch obrotowy jednostajnie przyspieszony, z drugiej zasady dynamiki dla ruchu obrotowego:
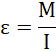
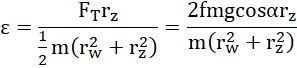
ponadto:
czyli:
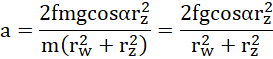
po przyrównaniu do siebie równości:
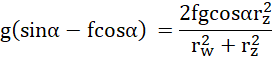
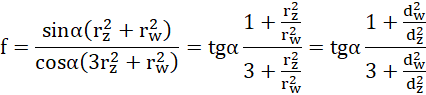
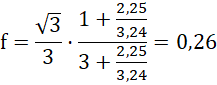
ponieważ jest to przypadek graniczny, prawdziwa jest nierówność:
Odpowiedź: Aby ruch odbywał się bez poślizgu, współczynnik tarcia statycznego musi być większy bądź równy od 0,26.
Najpierw zastanów się jakie siły działają na krąg – jest to siła ciężkości (rozpisz ją na składowe), siła reakcji podłoża oraz siła tarcia. Siła reakcji podłoża równoważy się ze składową siły ciężkości wzdłuż osi y (prostopadłej do zbocza), a suma pozostałych sił, z drugiej zasady dynamiki dla ruchu postępowego, to iloczyn masy i przyspieszenia liniowego kręgu. Ciało wykonuje też ruch obrotowy jednostajnie zmienny (gdyż siła na niego działająca nie jest równoważona), więc przyspieszenie kątowe jest równe ilorazowi wypadkowej momentu sił (tutaj jest to siła tarcia) oraz momentu bezwładności. Aby ruch odbywał się bez poślizgu, siła tarcia musi być większa od składowej Fgx siły ciężkości. Zbadajmy przypadek, gdy współczynnik jest możliwie najmniejszy, dla każdej większej wartości nierówność będzie spełniona. Z zebranych już równości wyznacz przyspieszenie liniowe (przyspieszenie kątowe to iloraz przyspieszenia liniowego i promienia zewnętrznego), a następnie po przyrównaniu ich do siebie wyznacz szukany współczynnik f. Jeżeli dla ułatwienia przekształceń, tak ja w podanym rozwiązaniu, średnice zostały zamienione na promienie, powróć do podanych w treści danych.