Dane:
a = 20 cm = 0,2 m
b = 40 cm = 0,4 m
c = 60 cm = 0,6 m
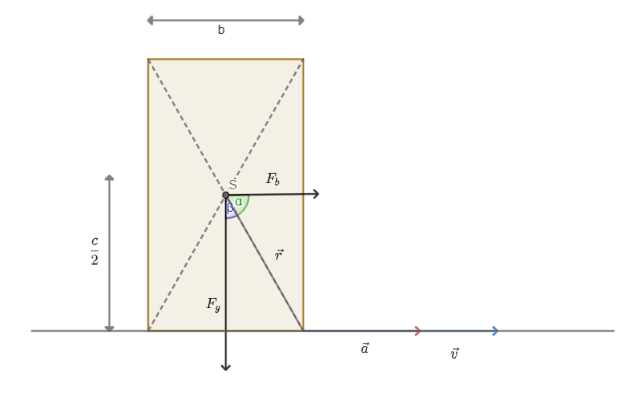
Rozpatrzmy nieinercjalny układ odniesienia.
Na walizkę działa siła ciężkości ![]()
![]()
Gdy ![]()
![]()
![]()
Gdy ![]()
![]()
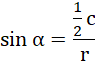
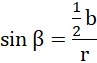
więc:
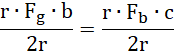
![]()
![]()
![]()
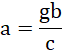
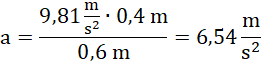
Odpowiedź: Walizka przewróci się, gdy przyspieszenie pociągu będzie większe niż ![]()

Pamiętaj, nieinercjalny układ odniesienia, to taki układ, który porusza się z pewnym przyspieszeniem względem pewnego innego układu odniesienia – w naszym przypadku wnętrze pociągu jest właśnie nieinercjalnym układem odniesienia. Zastanów się, jakie siły działają na walizkę – jest to siła ciężkości oraz siła bezwładności (nie uwzględniamy tarcia), aby walizka przewróciła się, siła bezwładności musi być większa od siły ciężkości. Wypiszmy momenty podanych sił w prawym dolnym rogu walizki – są to iloczyny danej siły, odległości od jej punktu przyłożenia i sinusa pomiędzy tymi wektorami. Zbadajmy przypadek graniczny, czyli przyrównajmy do siebie wartości obu momentów sił, zastąp sinusy stosunkami odpowiednich wartości wektorów (posiłkuj się własnym, bądź przygotowanym w rozwiązaniu rysunkiem) oraz w miejsce siły grawitacji wpisz iloczyn masy i przyspieszenia ziemskiego, a siły bezwładności – iloczyn masy i przyspieszenia pociągu (nasza szukana). Wyznacz szukaną wartość przyspieszenia, walizka przewróci się, gdy przyspieszenie pociągu będzie większe od otrzymanego wyniku, czyli gdy przekroczy wartość graniczną.