Dane:
f = 15 ![]()
n = 75
W = 43,3 J
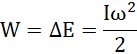
oraz:
![]()
czyli:
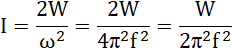
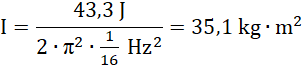
Prędkość malała liniowo, więc przyspieszenie było stałe.
Z drugiej zasady dynamiki dla ruchu obrotowego:
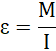
![]()
ponadto z zależności:
![]()
![]()
![]()
![]()
oraz:
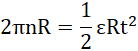
mamy:
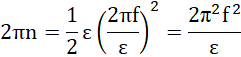
![]()
co daje:
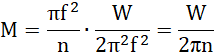
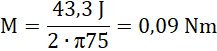
Odpowiedź: Moment bezwładności wentylatora wyniósł ![]()
![]()

Pamiętaj, wartość pracy to wartość przyrostu (zmiany) energii – w tym przypadku energii ruchu obrotowego. Wykorzystując zależność między prędkością kątową a częstotliwością, wyznacz moment bezwładności. Część wiatraka wykonuje ruch obrotowy jednostajnie opóźniony, więc z drugiej zasady dynamiki dla ruchu obrotowego, jej przyspieszenie kątowe jest równe ilorazowi momentu siły hamującej i momentu bezwładności. Zapisz także równanie opisujące ten ruch, zauważ, prędkość końcowa jest równa zero. Wyznacz z niego czas ruchu, który wykorzystasz w równaniu opisującym drogę liniową – kąt, jaki wykonała końcówka wiatraka (n pełnych obrotów) jest równa połowie przyspieszenia liniowego (zapisz jako iloczyn przyspieszenia kątowego i promienia) pomnożonej przez czas do kwadratu. Wstawiając odpowiednie równości i wykonując konieczne przekształcenia, wyznacz wartość przyspieszenia kątowego. Otrzymany wynik pomnóż przez moment bezwładności – otrzymasz szukany moment siły.