Dane:
m = 75 kg
R = 1,6 m
α = 3°
t = 10 s
Kula, staczając się, wykonuje ruch postępowy oraz ruch obrotowy
Na kulę działa siła ciężkości, siła tarcia i siła reakcji podłoża.
Rozpisując siłę ciężkości na składowe:
![]()
![]()
![]()
![]()
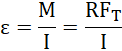
Moment bezwładności sfery: ![]()
Ponadto:
![]()
więc:
![]()
co daje:
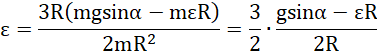
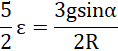
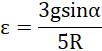
![]()
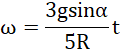
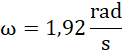
Odpowiedź: Prędkość kątowa kuli po 10 sekundach wyniosła ![]()

Zastanów się, jakie siły działają na kulę – są to siła ciężkości, siła reakcji podłoża oraz siła tarcia. Rozpisując siłę ciężkości na składowe, zauważ, że jedna z nich równoważy się z siłą reakcji podłoża. Wypadkowa pozostałych sił to z drugiej zasady dynamiki dla ruchu postępowego, iloczyn masy i przyspieszenia. Kula obraca się, więc z drugiej zasady dynamiki dla ruchu obrotowego, przyspieszenie kątowe jest równe ilorazowi wypadkowej momentu sił (tutaj jest to moment siły tarcia) i momentu bezwładności sfery (odczytaj z tabeli na końcu zbioru zadań). Wykorzystaj zależność między przyspieszeniem kątowym i przyspieszeniem liniowym, by wyznaczyć z zebranych równości siłę tarcia, którą następnie wykorzystaj do wyliczenia przyspieszenia kątowego. Wartość sinusa odczytaj z tablic trygonometrycznych. Pamiętaj, prędkość kątowa to iloczyn czasu trwania ruchu oraz przyspieszenia kątowego.