Oblicz prędkość kątową kręgu na końcu ruchu, wiedząc, że krąg o masie 530 kg, którego wymiary to: dw = 1500 mm– średnica wewnętrzna kręgu, dz = 1800 mm – średnica zewnętrzna kręgu toczy się bez poślizgu, po stoku długości 80 m, którego nachylenie wynosi 30°. Przyjmij, że 
Dane:
m = 530 kg
l = 80 m
dw = 1500 mm = 1,5 m
dz = 1800 mm = 1,8 m
α = 30°
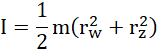
dla ułatwienia przekształceń, niech:
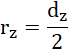
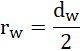
Z zasady zachowania energii:
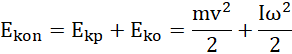
ponadto:
więc:
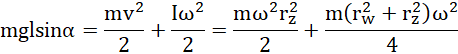
po przekształceniach:
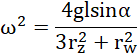
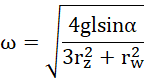
zamieniając promienie na średnice:
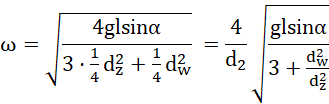
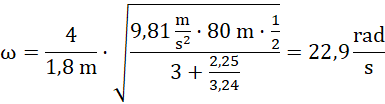
Odpowiedź: U podnóża krąg osiągnął prędkość kątową 
Skorzystaj z zasady zachowania energii – wartość na szczycie jest taka sama jak wartość u podnóża. Na szczycie krąg posiada jedynie energię potencjalną (czyli iloczyn masy, przyspieszenia grawitacyjnego oraz wysokości od podłoża – wykorzystaj podane w treści długość stoku i kąt nachylenia). U podnóża krąg posiada energię kinetyczną ruchu postępowego (iloczyn połowy masy i kwadratu prędkości liniowej) oraz energię kinetyczną ruchu obrotowego (iloczyn połowu momentu bezwładności i kwadratu prędkości kątowej). Zamień prędkość liniową na iloczyn prędkości kątowej i promienia zewnętrznego kręgu. Wyznacz i wylicz wartość prędkości kątowej. Jeżeli dla ułatwienia przekształceń średnice kręgu zostały zastąpione przez promienie, nie zapomnij zapisać końcowego wyrażenia z wykorzystaniem podanych w treści danych.