Oblicz czas, po którym kula będzie poruszać się bez poślizgu, wiedząc, że w chwili wyrzucenia jej przez zawodnika jej prędkość liniowa to v0 = 7 
Dane:
v0 = 7 
μ = 0,2
Niech:
R – promień kuli
m – masa kuli
v – prędkość liniowa kuli w momencie granicznym
Badamy przypadek graniczny, czyli moment, w którym kula zaczęła się poruszać bez poślizgu.
Kula obraca się, więc:
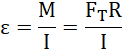
Moment bezwładności kuli: 
ponadto 
więc:
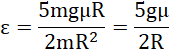
Korzystając z zależności:
otrzymujemy:
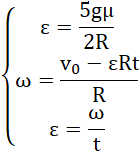
wykonując dalsze przekształcenia:
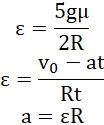
po wyznaczeniu ε i przyrównaniu do siebie wyrażeń:
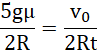
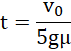
Odpowiedź: Kula zaczęła się poruszać ruchem bez poślizgu po 0,7 s.
Zbadaj przypadek graniczny, czyli moment, w którym kula zaczęła toczyć się bez poślizgu. Wykonuje ona ruch obrotowy, więc z drugiej zasady dynamiki dla ruchu obrotowego, jej przyspieszenie jest równe ilorazowi momentu siły tarcia i momentu bezwładności kuli. Jej prędkość liniowa zmalała w porównaniu z wartością prędkości nadanej przez zawodnika – jest to ruch jednostajnie opóźniony. Wykorzystując zależności pomiędzy prędkością i przyspieszeniem kątowym oraz liniowym, posługując się wzorem na prędkość liniową i przyspieszenie kuli, wyznacz czas trwania ruchu.