Dane:
l = 1 m
niech:
m – masa rurki
FN – siła naciągu nitki
a – przyspieszenie liniowe
r – promień rurki
Na rurkę działa siła grawitacji oraz siła naciągu nitki.
![]()
Rurka została wprawiona w ruch obrotowy, z 2 zasady dynamiki ruchu obrotowego dla bryły sztywnej:
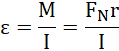
Moment bezwładności rurki: ![]()
Ponadto:
![]()
więc:
![]()
co razem z pierwszą równością daje:
![]()
![]()
Następnie:
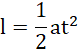
więc:
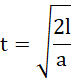
![]()
Odpowiedź![]()
![]()
![]()

Zastanów się, jakie siły działają na rurkę – są to siła grawitacji działająca w dół oraz siła naciągu nitki działająca w górę. Ich wypadkowa to iloczyn masy i przyspieszenia liniowego. Ponadto rurka obraca się, więc z 2 zasady dynamiki dla ruchu obrotowego bryły sztywnej, przyspieszenie kątowe jest równe ilorazowi momentu siły (czyli iloczynowi siły naciągu i promienia rurki) oraz momentowi bezwładności rurki (odczytasz go z tabeli na końcu zbioru zadań). Wykorzystując zależność między prędkością kątową a liniową, wyznacz wartość siły naciągu. Z otrzymanym wynikiem wróć do pierwszej równości – wyliczysz przyspieszenie liniowe. Aby poznać czas spadku, wykorzystaj wzór na drogę w ruchu liniowym jednostajnie zmiennym.