Dane:
mp = 355 g = 0,355 kg
d = 6 cm = 0,06 m
mc = 50 g = 0,05 kg
Niech oś X układu współrzędnych będzie zwrócona poziomo w prawo, a oś Y – pionowo w dół.
Przyspieszenie liniowe puntu na obwodzie puszki i dla ciężarka są takie same.
Na puszkę działa siła tarcia oraz siła naciągu nici.
Z drugiej zasady dynamiki w ruchu postępowym:
![]()
Niezrównoważona siła tarcia wprawia puszkę w ruch obrotowy jednostajnie przyspieszony.
Z drugiej zasady w ruchu obrotowym:
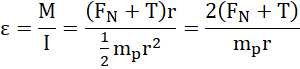
ponadto:
![]()
co daje:
![]()
Na ciężarek działa siła ciężkości oraz siła naciągu nici.
Z drugiej zasady dynamiki w ruchu postępowym:
![]()
Z równania (1) i (2):
![]()
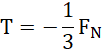
wstawiając do równania (1):
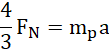
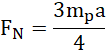
wstawiając do równania (3):
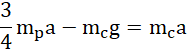
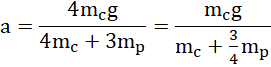
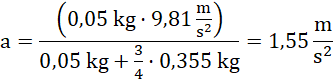
Odpowiedź: Przyspieszenie ciężarka wyniosło ![]()

Na początek ustal zwroty osi układu współrzędnych, ma to wpływ na to, które wartości pojawią się z minusem (przeciwny zwrot), a które z plusem(zwrot zgodny ze zwrotem osi). Następnie, wykorzystując do tego rysunek z poprzedniego Podpunkt:u, zastanów się, na jaki ruch wpływają poszczególne siły. Różnica siły naciągu liny i tarcia z drugiej zasady dynamiki dla ruchu postępowego to iloczyn przyspieszenia liniowego i masy puszki. Z kolei z drugiej zasady dynamiki dla ruchu obrotowego, iloraz wypadkowej momentu sił (suma momentów siły tarcia i naciągu liny) i momentu bezwładności to przyspieszenie kątowe puszki. Różnica pomiędzy siłą naciągu nici a siłą ciężkości ciężarka to zaś iloczyn przyspieszenia liniowego i masy ciężarka. Przyspieszenie liniowe jest takie same dla obu ciał, gdyż są połączone nierozciągliwą nitką. Z zebranych równań wyznacz najpierw siłę tarcia, następnie siłę naciągu, co doprowadzi Cię do szukanego przyspieszenia.